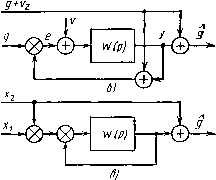Покажем, что ошибка описанной комплексной системы, одновременно являющаяся ошибкой радиотехнического измерителя, не зависит от задающего воздействия. Для этого представим ее схему в эквивалентном, но более развернутом виде, как показано на рис. 8.11,6. Видно, что задающее воздействие подается сразу на оба входа элемента сравнения (дискриминатора): на один вход непосредственно, а на другой - через цепь главной обратной связи. Поэтому изменение задающего воздействия не вызовет изменения ошибки e{t) и, следовательно, изменения выходной величины радиотехнического измерителя y{t). Однако в выходную величину комплексной системы§() воздействие g(f) полностью войдет из сигнала нерадиотехнического датчика.

Не реагируя на изменение задающего воздействия, контур радиотехнического измерителя в то же время будет подавлять погрешность нерадйотехнического датчика V2{t), поскольку в выходную величину у (t) будет добавляться составляющая, противоположная (t) по знаку. Это становится особенно на- глядным, если схему подвергнуть дальнейшим эквивалентным преобразованиям в соответствии с рис. 8.11, в, г, д.

На рис. 8.11,6 суммирование сигнала (t) с сигналом у (t) заменено. его вычитанием из сигнала Xi(t), что позволило освободить замкнутый контур радиотехнического изме-)ителя от дополнительных связей, а рис. 8.11, г он заменен одним динамическим звеном с передаточной функцией F{p)==W{p)/U + 4-1Г(р)], т. е. введена в рассмотрение передаточная функция замкнутой системы.

Схема, изображенная иа рис. 8.11, г, называется схемой компенсации и работает следующим образом. После вычитания сигнала X2it) = =g(t)+V2{t) из сигнала Xi(t)=g{t)+v(t) задающее воздействие компенсируется и остается аддитивнаясмесь погрешностей v(t)-V2(t). Эта смесь подается на фильтр с передаточнойфункцией F(p), хорошо пропускающий погрешность Vi(t), но подавляющий погрешность v(t). Поэтому на выходе фильтра получается хорошая оценка погрешности

l-F(pl

нерадиотехнического датчика со знаком минус. При ее суммировании с сигналом нерадиотехнического датчика X2(t) погрешность U2{t) почти полностью компенсируется, что обеспечивает высокую точность измерения. От схемы компенсации легко перейти к эквивалентной ей двухканальной схеме фильтрации, изображенной на рис. 8.П,5. Как и следовало ожидать, для нее выполняется условие (8.13), т. е. рассматривается комплексная система, действительно инвариантная по задающему воздействию.

Заметим, что сигнал Xi{t) представляет собой не выходной сигнал радиотехнического измерителя, а ненаблюдаемую смесь задающего и возмущающего воздействий, приложенную к входу. Возмущающее воздействие v(t] остается тем же, что и в некомплексной системе радиоавтоматики, и его можно считать белым шумом. В отличие от него погрешность нерадиотехнического датчика У2 (О обычно является весьма низкочастотным случайным процессом. Такое различие в спектрах логрешностей - необходимое условие выигрыша в точности при комплексировании. Низкочастотный фильтр с передаточной функцией F(p) при этом хорошо подавит погрешность v(t), высокочастотный фильтр с передаточной функцией 1-Р(р) - погрешность У2(0> а задающее воздействие пройдет на выход без искажений за счет параллельного включения фильтров.

В общем случае нерадиотехнический датчик может не быть безынерционным звеном и иметь произвольную передаточную функцию

Щ(Р) м+ь

VJz(Pi

Рис. 8.12

Wj2{p)- Тогда его сигнал необходимо сначала пропустить через фильтр с передаточной функцией

2(р)=1/д2(р) (8.14)

(если он реализуем), а затем уже вводить в контур радиотехнического измерителя, как в схеме на рис. 8.11, а. Однако тот же результат часто достигается проще, если входящие в контур элементы удается разбить на две части с передаточными функциями Wx{p) и Wip), причем Wi{p)W2{p) = W{р), и перенести точку введения сигнала нерадиотехнического датчика так, как показано на рис. 8.12. Равенство (8.14) служит условием инвариантности для схемы, изображенной на этом рисунке. Эта схема особенно характерна для случая, когда нерадиотехнический датчик вырабатывает производную задающего воздействия. Тогда звено с передаточной функцией 12(0) - интегратор, обязательно имеющийся в контуре астатической следящей системы.

Анализ точности и синтез комплексных систем. Будем считать, что погрешность нерадиотехнического датчика У2 (О - стационарный случайный процесс с известной спектральной плотностью 5 2(w). Возмущающее воздействие v(t), приведенное ко входу радиотехнического измерителя, как обычно считаем белым шумом с известным уровнем спектральной плотности Sj,{(o)=N. Взаимная, корреляция между процессами v{t) и U2{t) отсутствует, так как они имеют различную физическую природу.

Имея в виду двухканальную комплексную систему в виде замкнутого контура, отметим, что, как было показано выше, при любых передаточных функциях W{p) в ней выполняется условие инвариантности. Поскольку в инвариантной системе задающее воздействие не влияет на величину ошибки, его свойства не представляют интереса при анализе точности измерения. Не имеет значения также наличие или отсутствие взаимной корреляции процессов и v{t] или Viit).

Исходя из изображенной иа рис. 8. И, д эквивалентной схемы фильтрации, для спектральной плотности ошибки измерения запишем формулу

S, И = I 1 - f (/со) 1 (со) + I f (/со) 2 iV. (8.15)

Подставив в (8.15) выражение для передаточной функции замкнутой системы F{p) через передаточную функцию разомкнутой системы W{p), получим

5.И= г+жм тхта (8-16)

W (/о,)

1 + W (/ш)

Средний квадрат ошибки измерения найдем как интеграл от спектргль-ной плотности (8.16) по частоте

- 00 - Q0

Здесь А/э- эквивалентная полоса пропускания замкнутой системы.

Легко убедиться в том, что выражение (8.17) можно получить также из выражения (3.60) для среднего квадрата ошибки в некомплексиой системе, если заменить в нем спектральную плотность задающего воздействия Sg(cu) на спектральную плотность погрешности нерадиотехнического датчика 5,2(со). Ведь в соответствии со схемой компенсации на рис. 8.11, г фильтр с передаточной функцией F (р) выделяет погрешность нерадйотехнического датчика V2{t) из смеси -zM{t)-\-v{t], а в некомплексной замкнутой системе такой фильтр должен выделять задающее воздействие g{t) из смеси g{t]+u{t).

Сделанный вывод указывает на то, что применительно к комплексным системам можно использовать методы синтеза и оптимизации, развитые для обычных замкнутых автоматических систем, если формально считать задающим воздействием погрешность нерадйотехнического датчика. В частности, при оптимизации комплексной системы по критерию минимума среднеквадратичной ошибки можно воспользоваться методом оптимальной линейной фильтрации. Если спектральная плотность S{(i>) достоверно не известна, эффективным оказывается синтез робастных комплексных систем.

Особо следует остановиться на случае, когда задающее воздействие имеет шд, git)=gi{t)-]rg2it), причем на радиотехнический измеритель оно поступает полностью, а на нерадиотехнический датчик-лишь одна его составляющая git). Такая ситуация характерна при сопровождении движущейся радиолокациоииой цели посредством РЛС, установленной на движущемся объекте. При этом составляющая (О вызва-