со и произвольной начальной фазой ф. Максимальное значение первой производной такого воздействия составит max g(t] = max {gioix

XCOS (ш/-Ьф)}=ёГтах , ВТОрОЙ ПрОИЗВОДНОЙ - шзх (f) = шзх {-gn,ax X

X (и sin {(iit-i-(ii]}=gmax(- Поскольку ОНИ ДОЛЖНЫ быть ограничены величинами g-max Ип,ах. СПраВСДЛИВЫ НераВСНСТВа ёГтах тах, ёГтах <

ёГтах- Отсюда ЯСНО, ЧТО амплитудз задающего воздействия не может

быть произвольно большой И должна удовлетворять условиям gmax <gmJ( и ёГтах<Гтах/ -

Объединяя два последних неравенства в одно с учетом того обстоятельства, что gmax / <max/< при й<ёГтах/ёГтах> ПОЛуЧИМ СЛСДуЮЩуЮ

зависимость допустимой амплитуды гармонического задающего воздействия от его частоты:

I imax imax \ i ётах/ ПрИ Ш < СО,

min<i -, --у-

ёГтах/ при

(8.4)

где й)1=ёГгаах/ктах-

Если ш<(1)1, то при оценке хмаксихмальной возхможной ахмплитуды задающего воздействия существеиио ограничение его первой производной, если (й>-(Й1- второй производной. Если (й=(й1, то при хмак-симальиой возможной амплитуде воздействия достигнут предельно больших значений амплитуды первой и второй его производных.

Амплитуду ошибки обработки описанного гармонического задающего воздействия найдем с помощью модуля частотной передаточной функции для ошибки:

gmax

-Г(/ш)

(8.5)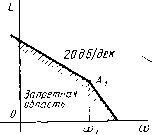

Рис. 8.6

При значениях частоты ш, лежащих в пределах полосы пропускания системы, когда lW(/ (]o)l, выражение (8.5) практически совпадает с выражениеме, зх=ётах/1*Следовательно, должно выполняться условие

п,а.х/ W(/ffl)l<eU. (8.6)

Из (8.6) и (8.4) получим требование к частотной передаточной функции разохмкнутого контура системы

Umax/(emax ) ПрИ Ш > Ш.

(8.7)

Неравенство (8.7) можно отобразить запретной областью на плоскости ЛАХ разохмкиутой системы L((]0)=20 lglF(/(]0) дБ. В соответствии с его правой частью граница этой запретной области образуется двумя прямыми с нак тонами -20 дБ/дек при (а<щ и -40 дБ/дек

при co>-coi. Точка излома А, имеет координаты

,=4!H2L, L(Q)i) = 201g-

gmax S max gmax

Описанная запретная область показана на рис. 8.6. Заметим, что поскольку при выводе (8.7) сделано предположение \W{j(o)\\, рассматривается лишь верхняя часть плоскости ЛАХ выше уровня О дБ.

Смысл построенной запретной области состоит в следующем. Если ЛАХ разомкнутой системы заходит в ее пределы, то существует такое гармоническое задающее воздействие, которое приводит к недопустимо большой динамической ошибке управления, превышающей значение 6?Tiax- Следовательно, при синтезе системы ее передаточная функция должна быть выбрана так, чтобы низкочастотная часть ЛАХ обязательно проходила выше границы запретной области.

Можно показать [3], что если учитывать задающие воздействия произвольной формы, а не только гармонические, то динамическая ошибка способна превысить значение даже в том случае, когда неравенство (8.7) выполняется, но близко к равенству. Чтобы гарантировать получение требуемой точности при произвольной форме задающего воздействия, следует несколько поднять границу запретной области для ЛАХ, однако весьма незначительно (примерно на 3 дБ). Поэтому в первом приближении можно считать, что прохождение ЛАХ за пределами запретной области, соответствующей неравенству (8.7), является не только необходимым, но и достаточным условием ограничения динамической ошибки величиной еах-

Аналогично производят построение запретной области для ЛАХ разомкнутой системы и в том случае, когда известны не максимальные, а среднеквадратичные значения первой ffg и второй производных задающего воздействия, а требование по точности состоит в том, чтобы среднеквадратичное значение динамической ошибки не превышало некоторого допустимого значения а?. Форма запретной области при этом совпадает с изображенной на рис. 8.6, а координаты точки излома А, составляют

1 = , L(co,) = 201g

ОеО.

Ограничение суммарной ошибки. Под суммарной ошибкой управления понимают сумму динамической ошибки и ошибки от во31ущаю-щего воздействия. Приведенное ко входу системы возмущающее воздействие будем считать белым шумом с известным уровнем спектральной плотности N, соответствующим наиболее тяжелой помеховой обстановке, в которой система радиоавтоматики должна нормально работать. Тогда среднеквадратичная ошибка от возмущающего воздействия составит

о,=\~Щ (8.8)

где А/э- эквивалентная полоса пропускания замкнутой системы для белого шума, выражаемая формулой (3.50). Возмущающее воздействие считаем некоррелированным с задающим воздействием.

Пусть требуется синтезировать систему таким образом, чтобы среднеквадратичная суммарная ошибка сг = K crg+(j не превышала некоторой заданной допустимой величины ст. Эта задача более сложна, чем ограничение только среднеквадратичной динамической ошибки Ogg, так как здесь предъявляются противоречивые требования к передаточной функции системы. С одной стороны, сохраняют силу условие (8.7) и изображенная на рис. 8.6 запретная область для ЛАХ, так как среднеквадратичная динамическая ошибка не только не должна превышать значения о°, но не может и достигать его - иначе даже при малой ошибке от возмущающего воздействия требования к суммарной ошибке будут нарушены. Однако среднеквадратичная ошибка от возмущающего воздействия также ие должна достигать о , т. е. с учетом форхмулы (8.8) эквивалентная полоса пропускания должна удовлетворять условию

А/э < (8.9)

Если одновременное вьшолиеиие условий (8.7) и (8.9) невозможно, то задача синтеза робастной системы при заданном значении ст ие имеет решения.

Выясним, при каких ЛАХ разомкнутой системы не может быть выполнено условие (8.9). Для зтого рассмотрихм типовые ЛАХ, низкочастотные отрезки которых содержат асимптоты с наклонами -20, -40 или -60 дБ/дек, но вблизи частоты среза обязательно имеется достаточно протяженный участок с наклоном -20 дБ/дек, вследствие чего обеспечивается хороший запас устойчивости замкнутой системы. Можно показать [3], что для системы с такими ЛАХ эквивалентная полоса пропускания с хорошей точностью оценивается по формуле

А/э со 2. (8.10)

Здесь (Во- так называемая базовая частота, соответствующая точке пересечения асимптоты ЛАХ с наклоном -/ 20 дБ/дек и оси абсцисс, а коэффициент / равен 1,2 или 3 в зависимости от наклона асимптоты, для которой определяется базовая частота.

Из (8.9) и (8.10) для базовой частоты получим неравенство

co <2(a )2/(/iV), (8.11)

определйющее допустимое крайнее правое положение асимптоты ЛАХ с наклоном -/ 20 дБ/дек. Его можно использовать при построении запретной области для ЛАХ, обеспечивающих выполнение условия (8.9). Для зтого на оси абсцисс надо отметить точки о ==2((j )ViV, ©о =сОо/2, со =сОо/3 и провести через них прямые с наклонами соот-ветствеиио -20, -40 и -60 дБ/дек так, как это сделано на рис. 8.7. В результате получим границу запретной области в виде ломаной линии, точки излома которой Лг и Лз имеют координаты

Шо (оеУ т , \ 10 п 4шо 0,30((Т?) т / X oi С0г = -= Ь{щ)=\2дБ, 3=2 =-1-(соз)=21 дБ.

Если ЛАХ разомкнутой системы заходит в пределы описанной запретной области, то требование по точности управления .не будет