лой (7.42), удовлетворяет условию

l г/пер W = 0.

(7.45)

Из (7.45) и (7.42) ясно, что для устойчивости линейной импульсной системы должно выполняться условие

\Zt\< 1 (1 = 1, 2, /),

(7.46)

т.е. все корни характеристического уравнения l + lF(z)=0 должны лежать внутри области устойчивости, имеющей вид круга единичного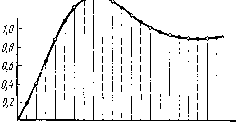

О 0,1 0,2 0,5 ОА 0,5 0,6 0,7 0,д 0,9 1,0 t,C Рис, 7.8

Рис. 7.9

радиуса на комплексной плоскости г. Она показана на рис. 7.9, а. Например, система с характеристическим уравнением первого порядка z+A = 0 будет устойчива при Л<:1.

При характеристическом уравнении более высокого порядка непосредственное использовавие условия (7.46) затруднительно. Однако исследование устойчивости существенно упрощается, если перейти к пу-преобразованию, описываемому соотношениями (7.12)-(7.14).

Учитывая, что г = e=cos соГ+/sin мГ, каждой точке окружности единичного радиуса в плоскости z с определенными координатами cos соГ и / sin аТ по вещественной и мнимой осям соответствует некоторая частота со из интервала от нуля до 2л/Г. Однако поскольку w = } ig со Г/2, при изменении со в указанном интервале изображающая точка в плоскости w движется по мнимой оси от нуля до ]оо и далее от -/оо к нулю, т. е. проходит вдоль всей мнимой оси. Поэтому окружность единичного радиуса, являющаяся границей области устойчивости в плоскости Z, при переходе к tw-преобразованию отображается в мнимую ось плоскости W. Область устойчивости в плоскости W лежит слева от мнимой оси, как показано на рис. 7.9, б, и совпадает по форме с областью устойчивости непрерывных систем, которая, напомним, лежит слева от мнимой оси плоскости р.

Это делает правомерным использование при исследовании устойчивости импульсных систем всех критериев устойчивости, разработанных применительно к непрерывным системам. Необходимо лишь перейти от переменной z к переменной w или, при использовании частотных критериев устойчивости, к псевдочастоте.

Пусть, например, система имеет характеристическое уравнение второго порядка

2 + 2 + 5 = 0. (7.47)

Посредством подстановки (7.13) оно преобразуется к виду {1 - А+В) w-2{\-B)w+l + A+B = 0.

Теперь можно воспользоваться алгебраическим критерием устойчивости. Как следует из критерия Гурвица (см. § 2.2), необходимым и достаточным условием устойчивости системы второго порядка является положительность коэффициентов ее характеристического уравнения. Поэтому система с характеристическим уравнением (7.47) будет устойчива лишь при выполнении неравенств

1 -Л+ 5> О,

В<1, [ (7-48)

1 + Л + В > 0. ,

пример 7.3. Найдем условие устойчивости для системы, рассмотренной в примере 7.1. Она имеет характеристическое уравнение

z+(K--l-d - Kd)z + d = 0.

Это уравнение совпадает с (7.47) при А = K~\-d - Kd, B = d. Поэтому с использованием ta-преобразования можно получить условие устойчивости в виде неравенств (7.48). Учитывая, что rf = exp (-Г/7 ) < I, только первое из этих неравенств налагает существенное ограничение на параметры системы. Оно дает условие устойчивости

Оценка качества управления. Показатели запаса устойчивости, быстродействия и точности импульсной системы, характеризующие качество ее работы, могут быть определены в результате построения кривой переходного процесса, а также посредством различных критериев качества.

При оценке запаса устойчивости особенно удобны частотные критерии. Например, склонность системы к колебаниям в переходном процессе-можно оценить по значению показателя колебательности М, введенного в § 2.3 как высота наибольшего пика нормированной АЧХ замкнутой системы. Как и в случае непрерывных систем, получение заданного показателя колебательности сводится к выполнению требования, чтобы АФХ разомкнутой системы не заходила в запретную область, окружающую точку (-1, /0) в соответствии с рис. 2.12. Крайняя правая точка этой запретной области лежит на расстоянии M/(M + 1) от оси ординат. При этом безразлично, построена ли АФХ в функции частоты ы или псевдочастоты Х.

Пример 7.4. Пусть дискретная передаточная функция разомкнутого контура импульсной системы имеет вид

W (z)=KiT/(z-l).

Выясним, как влияет величина Ki на показатель колебательности замкнутой системы М. Для этого, выполнив подстановку г = е, перейдем к частотной передаточной функции

-2sm-7;-l-/2sin-cos

2 sin

sin-ij-h/cos-jj-

В координатах (/= Re W и V = IrnW АФХ будет представлять собой вертикальную прямую линию, проходящую на расстоянии KiT/2 слева от оси ординат. Она показана на рис. 7.10. Там же штриховкой выделена запретная область по условию получения заданного показателя колебательности М.

Видно, что допустимое расположение АФХ соответствует неравенству

KiT/2<M/(M+\),

откуда

Ki<2M/lT(M+\)].

Для получения значения УИ = 1,3, свидетельствующего о малой колебательности системы, должно выполняться условие < 1,13/7 . Границе устойчивости системы соответствует величина /Ci, обращающая неравенство в равенство при М- со, т. е. /Ci = 2/r. Это ясно также из критерия устойчивости Найквиста, поскольку при таком Ki АФХ пройдет через точку с координатами (-1, /0).

АФХ импульсной системы имеет одну и ту же форму независимо от того, построена ли она в функции частоты со или псевдочастоты

однако логарифмические частотные характеристики целесообразно строить только в функции псевдочастоты. При этом методика оценки запаса устойчивости по ЛАХ разомкнутой системы L*{X) =

Рис. 7.10

Рис. 7.11

=20 \g\W*(i\)\ И ее ЛФХ vl5*(X)=arg не отличается от исполь-

зуемой при исследовании непрерывных систем. Удобным критерием является величина запаса устойчивости по фазе Дг1)=180°+г15*(Л,р), где >.£р - псевдочастота среза, на которой L*(>.cp)=0 или llF*(/cp)i = = Л*(>.ср) = 1- В системе с хорошим запасом устойчивости должно выполняться условие Дг15=(30-60)°. Заметим, что после нахождения псевдочастоты среза можно приближенно оценить также время переходного процесса в системе по формуле (510)/>.ср-