Практически обратное преобразование выполняют путем разложения Х2{р) на простейшие дроби с последующим использованием таблиц преобразований Лапласа.

Пример 1.1. Дано уравнение системы Tx2-\-x2. = kxi и входное воздействие 1 {t) = Xт sm Qt. Требуется определить процесс на выходе.

В соответствиис (1.5)получаем (t) = kxi (,t)/{l +Тр), откуда W (р) = й/(1 -\-Тр). По таблицам изображений Лапласа находим

Тогда

Разложим (р) на простейшие дроби:

1 А Bp С {А + ВТ) p + jB+CT) p + AQ + C

<l + rp)(p2+fl2) l+rpV + SV + (l + Tp){p + Q)

Приравнивая коэффициенты при одинаковых степенях р в числителе левой и правой частей этого равенства, получим систему алгебраических уравнений для определения коэффициентов:

А + ВТ=0, В--СГ=0, Лй2--С=1.

Откуда находим Л = В = Х , с=у.

Воспользовавшись таблицами изображений Лапласа, находим

L-1 L-1

Bp -

3 т

= BcosQt=-

-t/T

cosQ

~ Q * 1 + 2 Q

и окончательно получаем процесс на выходе системы

лга () = L-1 [2 (-y)l = 2п (О + л:2у (О =

йд:

1 -}- rQa

1 + rQa

(sin Qt-TQ cos QO,

лггп (0 = kx

1 + r2Q2

ay (0 = 1; ,, (sin - cos QO.

Использование переходной и весовой функций. Переходная функция служит для оценки качества работы автоматической системы в переходном режиме. Переходной функцией линейной динамической системы называют отклик этой системы на единичную ступенчатую функцию, определяемую как

( О при < О,

< =Unp ,>o.

При заданном дифференциальном уравнении линейной динамической системы ее переходную функцию наиболее просто определить следующим образом. Записав дифференциальное уравнение в символической форме и обозначив переходную функцию q{t), получим из (1.5)

q{t) = W(p)lit). (1.18)

Перейдем в область изображений по Лапласу: Qip) = W(p)I(p),

I{p) = L[l(t)] = l/p.

Откуда, используя таблицы преобразования Лапласа и снова переходя во временную область, получим

jW(p)

1(0-

(1.19>

Необходимость умножения на 1 (t) функции, полученной в результате обратного преобразования Лапласа, обусловлена тем, что переходная функция как реакция на воздействие, отличное от нуля лишь при tO, равна нулю при /<0, т. е. 9()=0при <0, что и обеспечивается вЬедением множителя \(t).

qlt) 7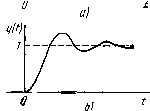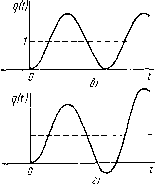

Рис. L.13

Графическое изображение переходной функции называют переходной характеристикой. Типовые переходные характеристики автоматических систем приведены на рис. 1.13. Кривые на рис. 1.13, а, 5 соответствуют устойчивой системе, кривые на рис. 1.13, б, г - неустойчивой.

Пример 1.2. Пусть система описывается уравнением {Tp4-[)y = kg или у (t)~ k d k

g(t), где Р - -ТГ Тогда передаточная функция Н = , -г P=+i<

1 + Гр и Q(P) =

+ Тр) [р

1 + Тр

\+Тр

Отсюданаходим

q{t) = L-[Q(p)\=kJL-

= k {1 1 (t)] = k(\-e-*l) 1 (t).

Весовой функцией линейной системы называют отклик этой системы на единичную дельта-функцию, которая может быть определена как производная единичной ступенчатой функции:

/ Л1 (п f О при t ф(),

б(0 = = Г (1.20)

dt \оо при = 0,

причем 5 b{tj) dti = l [t] и 5 8{t)dt=l для любых а, р>0. Эту функ-

-00 -а

цию иногда называют функцией веса.

Дельта-функция обладает фильтрующим свойством, предельно упрощающим вычисление определенных интегралов, в подынтегральное выражение которых эта функция входит как сомножитель

ti + b

л S f{t)6{t,-t)di = f{t,) (1.20а)

.при любых 0<а, b-f оо для любой ограниченной функции f(t). Кроме того, для любой ограниченной функции f{t) имеет место равенство f {t)6(t)=f(0)6(t), если /(0)0, и /(06(0=0, если /(0)=0.

Записав дифференциальное уравнение линейной динамической системы в форме (1.5), с учетом (1.18) и (1.20) получим

w{t) = W ip) 6(t) = W ip)p\ it) = pW (p) 1 (t) = pq{t)=. (1.21)

Таким образом, функция веса динамической системы равна производной переходной функции этой системы. Поскольку функция w (t) - реакция динамической системы на воздействие, приложенное к ее входу в момент времени =0 и отсутствующее при <0, а никакая реальная система не может реагировать на входное воздействие до того, как оно поступило на ее вход, ясно, что для всякой реальной динамической системы w(t)=0 при <0. Требование

ш(0-0 при < О (1.22)

.называют условием физической реализуемости системы. Поэтому в каждом частном случае, когда весовой функцией системы является некоторая конкретная функция времени f{t), которая определена для всех t в интервале (-oo, -f оо) и не равна нулю при <0, весовая функ-

€4ия

°7/(0 при tO, ()=!о при t<0, (1-23)