Максимальное значение шума квантования составляет 8J2. Дисперсия этого шума, если допустить, что уровень его плотности вероятности в интервале от -до +6i/2 постоянен,

0 = j v\b-,v, = . (7.25,

-б,/2

Корреляционная функция шума квантования 7?б, Irn] затухает тем быстрее, чем меньше величина 6i по сравнению со среднеквадратичным приращением (из.менением) входного сигнала за время, равное периоду дискретности Т. Можно показать, что при выполнении условия

б, < 2,2Т(Т. , (7.26)

где (Tg - среднеквадратичное значение производной входного процесса, корреляционная функция Rv\m\ отлична от нуля практически только при т = 0, так как уже при /п = 1 ее значение пренебрежимо мало и составляет /?о, [110,01 7? J0]. Тогда для корреляционной функции шума квантования справедливо выражение

/? [т] = 0,ЛИ> (7.27)

где бо [/п] - единичная импульсная решетчатая функция.

Решетчатый случайный процесс с корреляционной функцией вида (7.28) называют дискретным бглы.м шумом. Его спектральную ллотность в соответствии с формулой (7.17)

5 (г)= 2 /? Иг- = 7? [0] = О,1.

т = -оо

При переходе к частоте со и к псевдочастоте по фэрмула.м (7.18), <7.20) спектральная плотность не изменяется и с учетом (7.25)

S;, {Ц = (е 0 = (г) = = 6f/l 2. (7.28)

Таким образом, при выполнении условия (7.26) шум квантования по уровню во входном АЦП можно считать дискретным белым шумом с равномерной спектральной плотностью.

Форма статической характеристики выходного ЦАП совпадает с изображенной на рис. 7.3, но по оси абсцисс откладывается поступающая с ЦВМ цифровая величина, а по оси ординат - соответствующая ей выходная величина аналогового сигнала, которая может принимать лишь дискретныэ значения, кратные цене единицы младшего разряда ЦАП бз. При линеаризации ЦАП он, аналогично АЦП, заменяется линейным звеном с коэфф.циентом передачи б а, на выход которого добавляется дискретный белый шум vln] с дисперсией =61/12.

§ 7.2. ТЕОРИЯ ЛИНЕЙНЫХ ИМПУЛЬСНЫХ СИСТЕМ

Передаточные функции импульсных систем. Большинство импульсных систем радиоавто.магики мэж.тэ представить в виде замкнутого контура, показанного на рис. 7.1, где импульсный элг.менг вклю-

чен в канале ошибки непосредственно после элемента сравнения. Это соответствует импульсному режиму работы дискриминатора. Динамические свойства такой системы определяются ее приведенной непрерывной частью, которая изображена на рис. 7.5 как последовательное соединение формирующего элемента и непрерывной части с передаточной функцией Wsip)- При [рассмотрении выходной величины y(t) лишь в дискретные моменты времени г! = пГ приведенную непрерывную часть можно считать импульсным фильтром, основными характеристиками которого являются решетчатая весовая функция wuin] и дискретная передаточная функция Wn(z). Найдем эти характеристики.

Решетчатую весовую функцию приведенной непрерывной части определим как ее реакцию на единичную импульсную решетчатую функцию е [п]=бо[п1, пока занную на рис. 7.6. Там же показан при

е[п] 1

е[п]\

y(fl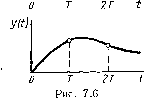

Рис. 7.5

мерный вид вызванных подобным входным воздействием функций e*(t) и y(t). Выходной сигнал формирующего элемента e*(t) является одиночным импульсом, в случае АИМ-1 имеющим прямоугольную форму. В общем случае форма импульса может быть произвольной. Выходной сигнал непрерывной части y(t) - непрерывная функция, являющаяся реакцией непрерывной части на одиночный импульс e*(t). Найдем ее по формуле свертки

y{t)]e*{%)w {t-%)d%, (7.29)

где ГУн(т) -весовая функция непрерывной части, связанная с передаточной функцией Wh(p) обратным преобразованием Лапласа: w{t) =

Решетчатая весовая функция wj.n\ получается в результате дискретизации во времени описываемого выражением (7.29) сигнала y{t), т. е. Wn[n]-=y{t)\t=nT-

Дискретную передаточную функцию приведенной непрерывной части найдем как г-преобразование весовой функции Wu{z)=Z {wa[n]\ или, в эквивалентной записи, Wn{z)=Z{Y{p)\, где К(р) - изображение по Лапласу функции y{t). Учитывая, что в соответствии с (7.29) функция y{t) является сверткой функций e*{f) и (t), ее изображение равно произведению изображений этих функций:

Yip)=FAp)WAp), (7.30)

где F{p)=L{e*{t)\ - язображент по Лапласу одиночного выходного импульса формирующего элемента.

Выражение (7.30) позволяет записать искомую дискретную передаточную функцию приведенной непрерывной части:

WAz)Z{FAp)WJpy}. (7.31)

Фактически полученное выражение (7.31) дает дискретную передаточную функцию разомкнутого контура системы, обозначаемую через W{z), так как кроме приведенной непрерывной части в системе нет других динамических звеньев, а идеальный импульсный элемент производит лишь дискретизацию сигнала рассогласования, не изменяя его значений. Если работа импульсного элемента соответствует АИМ-1 и импульс e*{t) является прямоугольным с единичной высотой и относительной деятельностью у, то для изображения F (р) получим

FAp)-}j e4t)exp{-pt)dt= j 1ехр(-рО=~ р~- 47-32)

При у<1 в формуле (7.32) можно приближенно принять ехр (-урТ);1-урТ, что дает F{p)=yT или при подстановке в (7.31)

W{z)yTZ{WAp)}. (7.33)

Формула (7.33) справедлива, если можно пренебречь влиянием конечной длительности импульса и считать короткие прямоугольные импульсы на выходе реального импульсного элемента эквивалентными по своему действию, на систему серии б-функций. Для этого обычно достаточно, чтобы в непрерывной части системы содержалось апериодическое звено с постоянной времени, превышающей длительность импульса.

Если интересоваться значениями выходного сигнала y(t) в смещенные по отношению к тактовым точкам моменты времени t={n+e) Т, 0<е< 1, товформулах (7.31) и (7.33) следует перейти к модифицированному 2-преобразованию. Тогда получим дискретную передаточную функцию

W (z, е) = Z, {F, (р) (р)} yTZ, {W, (р)}, (7.34)

связывающую изображения выходной величины и ошибки соотношением

Y{z, e)=W (г, е) Е (z, 0)=W {z, е)Е (z). (7.35>

Здесь изображение ошибки взято при е= О, так как импульсный элемент реагирует на ошибку лишь в тактовых точках.

Пример 7.Г. Найдем дискретную передаточную функцию разомкнутой системы W (z, Е) для случая, когда импульсный элемент осуществляет АИМ-1, а непрерывная часть имеет передаточную функцию

причем постоянная времени Т превышает длительность импульса х = уТ. 210