откуда найдем стохастическое дифференциальное уравнение для случайного задающего воздействия со спектральной плотностью (6.36):

d g (О

d -ig(0 , , dg(i)

, .1 ,-ао(0 = М(О- (6.38)

Запишем теперь (6.38) в форме уравнения состояния. Обозначим

(6.39)

тогда

x,{t) = dg/di> = x,Ath k=\,n-l.

(6.40)

Используем векторно-матричные обозначения для совокупностей переменных и коэффициентов:

X = [Xi, х, ...,

матрица-столбец размера пХ\, или п-вектор;

5 = [О, О.....Ьо]-

матрица-столбец размера пХ1;

(6.41) (6.42)

О О О

о о о

(6.43)

квадратная матрица размера пХп.

Тогда уравнение (6.38) запишем в виде одного матричного уравнения первого порядка [см. гл. 1, вывод уравнения (1.30)]:

dx/dt = Ax[{t) + Bu[{t), (6.44)

которое и является уравнением состояния для -мерного задающего воздействия x{t). Количество переменных состояния Xi, х, ... , х в этом уравнении определяется степенью полинома в знаменателе выражения (6.36) для спектральной плотности задающего воздействия g{t), которому в матрице [х, х, . . . , соответствует обозначение х.

Чтобы из совокупности п переменных состояния, содержащихся в матричном уравнении (6.44), выделить задающее воздействие g{t), необходимо (6.44) дополнить матричным уравнением вида

git)Cxit),

(6.45)

где С = [1, О, О, ... , 0] - матрица размера 1Хп.

Уравнения (6.44) и (6.45) являются исходными соотношениями для оптимального синтеза методом пространства состояний.

Заметим, что (6.38) является дифференциальным уравнением формирующего фильтра, возбуждаемого белым шумом u{t). На рис. 6.3 представлена схема набора на модели формирующего фильтра, соот-

ветствующая (6.38), которая может быть использована для получения случайного процесса с заданной спектральной плотностью при моделировании систем радиоавтоматики, работающих в условиях случайных воздействий.

Синтез фильтров Калмана. В общем случае фильтр Калмана представляет собой многомерный нестационарный следящий измеритель, т. е. систему с переменными параметрами. Нестационарность фильтра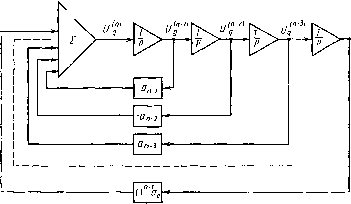

Рис. 6.3

Калмана обусловлена, во-первых, тем, что фильтр Калмана является оптимальным при конечном времени наблюдения, т. е. является оптимальным не только в установившемся, но и в переходном режиме, а во-вторых, тем, что задающее воздействие и помеха могут быть нестационарными случайными процессами.

Задача синтеза такого многомерного нестационарного фильтра состоит в следующем [2]. Дан случайный нестационарный п-мерный процесс x{t)=[xi{t), xit), . . . , Xn(t)], описываемый уравнением состояния

x{t) = A{t)x{t)-\-B{t)u{t), (6.46)

где u{t) - случайный г-мерный процесс типа белого шума, порождающий случайный процесс x{t)\ A{t) - квадратная матрица коэффициентов размера пХп\ B{f) - прямоугольная матрица коэффициентов размера пХг. В отличие от (6.44) коэффициенты уравнения (6.46) переменные, что является следствием нестационарности процесса x{t). Корреляционная матрица порождающего белого шума и () имеет

K.t, l) = u{t)u {l) = Q{t){t-l), (6.47)

где Q{t) - матрица размера rxr, элементы которой имеют размерность и смысл спектральных плотностей qu и взаимных спектральных плотностей qij составляющих Ui{t) и Uj{t) процесса u{t); б(-) - дельта-функция.

На вход синтезируемого фильтра поступает т-мерная совокуп-

ность наблюдаемых величин, имеющая смысл многомерного входного воздействия:

r{t)C{t)x{t)-v{t), (6.48)

где C{t) - матрица наблюдений размера mXn; v{t) - случайный m-мерный процесс типа белого шума (например, флуктуационные помехи в каналах связи) с корреляционной матрицей

K,AtA) = 4{t){t-l)\ (6.49)

здесь R (О - положительно определенная симметричная матрица размера mXm, для которой существует обратная матрица R~it).

Элементы матрицы R (t) имеют смысл и размерность спектральных плотностей Ра и взаимных спектральных плотностей ри, составляющих Vi{t) и Uj()m-MepHofi помехи v{t).

Оптимальный фильтр, имея на входе совокупность наблюдаемых величин r()=[ri(4, rit), . . . , rm{t)], должен дать оценку y{t) процесса .v-(/), оптимальную по критерию минимума среднеквадратичной ошибки измерений каждой из составляющих процесса x{t).

Выражение для критерия оптимума многомерного фильтра Кал-мана аналогично формуле (6.9) и имеет вид /й=ш1п е, k=l, п, где

elMxAt)-yn{t)Y.

Как доказывается в теории оптимальной фильтрации [8], оптимальная оценка y{t) процесса x{t) удовлетворяет п-мерному матричному дифференциальному уравнению (уравнение оценки)

dyldt A{t)y {t) + Kii) [г {t)~-C{t)y{t)], (6.50)

K{t)P{t)C{t)R-4t)~- (6.51)

матричный коэффициент передачи оптимального -мерного фильтра (фильтра Калмана);

P{t) = [x{t)-y{t)\[x{t)-~y{t)]~ (6.52)

дисперсионная матрица ошибок фильтра. Элементами последней матрицы являются величины

Dij it) - [X, (О-г/, (0] [/ {t)-yj (OJ

причем на главной , диагонали этой матрицы находятся дисперсии ошибок оптимального фильтра Dii{t) = [Xi{t)-yi{t)\=e].

Дисперсионная матрица ошибок P{t) определяется путем решения дисперсионного уравнения

= AP + PA-PCR-CP + BQB. (6.53)

Уравнение (6.53) - это матричное нелинейное дифференциальное уравнение Риккати. Для его решения необходимо задать начальное значение P{io) дисперсионной матрицы. Если в начальный момент времени ik процесс у (to) на выходе фильтра равен нулю, то, как