Рассмотренная методика может быть использована и для расчета других величин, однако в соответствии с изложенным при статистической линеаризации нелинейностей нужно рассматривать величину х, являющуюся входной величиной нелинейности (см. рис. 5.12).

Пусть динамика системы описывается уравнением, записанным для ошибки, вида

Q {р) e{t) + R ip) P{e) = Q (р) g (t), (5.42)

где e=g-у - ошибка системы {у - управляемая величина); Q(p) и R{p) - полиномы; F{e) - нелинейная функция; g - задающее воздействие.

Задающее воздействие равно сумме математического ожидания и случайной составляющей: g=g\-g. Ошибка системы тоже может быть представлена в виде такой суммы: е=е-]-е°.

Пусть в системе отсутствуют автоколебания. Тогда, применив статистическую линеаризацию (5.18) и подставив полученное выражение в (5.42), разобьем последнее иа два:

Qip)e+R{p)F = Q{p)i, (5.43)

[Q{p) + R{p)q>] = Q{p)g (5.44)

соответственно для регулярных и случайных составляющих задающего воздействия и ошибки. При этом F{e, 0) и q{e, Ge) определяют для каждой конкретной нелинейности в соответствии с изложенным.

В установившемся режиме g, е и Од оказываются постоянными. Тогда Уравнение (5.44) становится алгебраическим:

Q (0) ё+ R (0) F> , а,) = Q (0) g. (5.45)

В ypaBHenvie (5.45) входят две неизвестные величины е и Og. Таким образом, из этого уравнения может быть определена зависи.мэсть математического ожидания ошибю! как функшш среднеквадратичного значения случайной составляющей ошибки e{Gg).

Равенство (5.45) справедливо для статических систем. В астатических cvicTeMax QiP)=pQiip)- Это соответствует астатизму первого порядка. Тогда вместо (5.45) получим равенство

R{0)F{e:a,) = Q,{0)V. (5.46)

Здесь V - постоянное значение скорости изменения задающего воздействия.

Из (5.46) также может быть определена зависимость e{Og). Аналогичное уравнение может быть получено и при астатизме более высокого порядка.

В уравнении (5.44) случайная составляющая входного воздействия задана в виде спектральной плотности Sg (со) или корреляционной функции Kg (г). Тогда на основании vlЗЛoжeннoгo в гл. 3 может быть

найдена дисперсия случайной составляющей ошибки:

Q (/и)

S(M)dcu. (5.47)

Здесь в зависимости qcfie, Gg) надо заменить е найденной зависимостью е{Ое). Тогда в уравнении (5.47) остается одна неизвестная величина а. Интеграл в (5.47) может быть вычислен с помощью приложения 1, а затем определено значение о.

После нахождения может быть вычислено и математическое ожидание ошибки по ранее определенной зависимости е(ае). Таким образом, рассмотренная методика позволяет определить два первых момента ошибки в исследуемой системе.

Однако зависимость е{ае) не всегда можно найти из уравнений (5.46) и (5.47) в явном виде. Поэтому совместное решение уравнений для е и Ое приходится делать либо численно, для чего целесообразно использовать ЭВМ, либо графически.

При исследовании неустановившихся режимов, когда полезный сигнал управления меняется во времени, исследуемый процесс уже не будет стационарным. Однако в большинстве случаев полезный сигнал можно считать медленно меняющимся по сравнению с изменением во времени помехи. Тогда возможно в первом приближении исследовать случайный процесс как стационарный. Однако в этом случае нельзя использовать формулы (5.45) и (5.46), справедливые для установившегося режима, а следует воспользоваться дифференциальным уравнением (5.43). Как и в случае установившегося режима, совместное решение двух уравнений (5.43) и (5.47) может быть произведено на основе численных методов с использованием ЭВМ или графическим путем.

Рассмотрим существо этих методов. Уравнение (5.47) запишем в виде

Gjllila), (5.48>

где 1{е, 0е) - интеграл, определяемый по приложению!. Затем построим зависимость левой и правой частей (5.48) от Ое- Левая часть дает параболу / (рис. 5.18), а правую часть можно построить, задаваясь каждый раз постоянным значением е и вычисляя интеграл I {е, Og) (кривые 2). Перенеся абсциссы точек пересечения этих кривых на плоскость (а, е) и отложив для каждой из них соответствующие кривым 2 ординаты е, получим искомую зависимость Of,{e) в виде кривой 3.

Подставив полученную зависимость ае(е) в вычисленное для данной нелинейности выражение ~F{x, а), что в рассматриваемом случае дает F{e, Og), исключим из него величину о и получим функцию от одной переменной f=T)(e), которую можно назвать функцией смещения. Здесь математические ожидания е п F представляют собой сме-

щения центра случайных составляющих на входе и на выходе нелинейности.

Когда функция смещения найдена, ее можно подставить в дифференциальное уравнение (5.43):

Q{p)e+Rip)y]ie) = Q{p)g{t) (5.49)

и отсюда по заданной функции g{t) путем решения дифференциального уравнения найти регулярную составляющую ошибки.

Функция смещен>1Я обычно имеет вид плавной кривой (рис. 5.19), которую в некоторых пределах можно подвергнуть линеаризации:

Р = Кё={йУ]/йё)~ё. (5.50)

Тогда уравнение (5.49) оказывается линейным:

Q{p)~e + R (р) е = Q (р) g (О (5.51)

F= 71(e)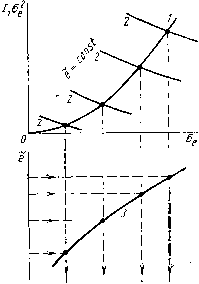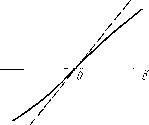

Рис. 5.18

Рис. 5.19

Часто встречается случай, когда линейная часть системы с передаточной функц>1ей R{p)/Q{p) не пропускает спектр частот, соответствующий случайной составляющей сигнала g и определяемый спектральной плотностью Sg(co). Тогда отыскание величины сГе знач>1тельно упрощается. Из (5.47) следует

= i f S(co)dco = D ,

(5.52)

т. е. не зависит от формы нелинейности и от величины е, а непосредственно равно дисперсии случайной составляющей g .

В этом случае вместо дифференцирования функции смещения (5.50) можно определить коэффициент передачи нелинейного звена непосредственно из выражения Р{х, сг,.), которое для ошибки имеет вид F{e, а). Тогда

F = kJ = {dF/d~e)~e. (5.53)

Здесь получаем как функцию от Од, т. е. k =k.,{ae).