Представив эквивалентный коэффициент передачи случайной составляющей в виде q=ca-(p{x, а), по формулам (5.23) и (5.25) находим соответственно

Ф1-/ 1-(4У-[Ф( 1) + Ф(1 2 1)з!Еп>а] . (5.35) Ф, = [ехр (- 0,5 ?) + ехр (- 0,5 1)]. (5.36)

Эти зависимости являются четными функциями величины х. Они изображены для случая х>0 на рис. 5.15, в, г.

В частном случае при х=0 из формул (5.35) и (5.36) можно получить соответственно

= Ф,(О,0,) = 1/1-Ф(6/а,),

/S = i/4exp(-l

(5.37) (5.38)

Для линейной характеристики с насыщением (рис. 5.16, а) имеем

.,Ф(.о+-Т~ф( )

[ехр (-0,5 )-ехр (- 0,5и1)].

(5.39)

Соответствующий график построен на рис. 5.16, б.

Функции, определяющие эквивалентный коэффициент передачи случайной составляющей по формулам (5.23) и (5.25), будут

--{u,expi-~0,5ul) + Uiexpi~0,5ul))\\ , (5.40)

Ф( 0 + Ф( 2) sign ,-

Ф2 = [Ф( 1) + Ф( .)з1Еп ,].

(5.41)

Графики полученных зависимостей изображены на рис. 5-16, в, г. Пример прохождения случайного сигнала через разомкнутую цепь.

Рассмотрим разомкнутую цепь (см. рис. 5.12), у которой передаточная функция линейной части соответствует апериодическому звену первого порядка W{p)=k/{\ + Tp), а нелинейное звено представляет собой безынерционный усилитель с характеристикой, изображенной на рис. 5.16, а. Зададим следующие исходные данные: =1, 7=0,1 с, зона линейности нелинейного звена по входу 6=1 В, максимальное значение сигнала на его выходе с=10В.

Пусть на входе действует полезный сигнал g в присутствии флукту-.ационной помехи, представляющей собой белый шум с интенсивностью

Л=0,8 ВГц. Требуется построить статическую характеристику совокупности двух звеньев y=fiig) с учетом подавления усиления, вносимого помехой, определить результирующий коэффициент передачи в точке g=0 и построить зависимость среднеквадратичного значения случайной составляющей сигнала на выходе нелинейного звена в функции значения полезного сигнала на входе Oy-fig).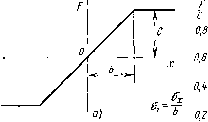

IB 12

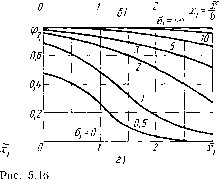В соответствии с изложенным в гл. 3 математическое ожидание выходной величины линейного звена в установившемся режиме x=/feg. Так как то x=g.

Дисперсия случайной составляющей на выходе линейного звена в соответствии с (3.25)

npvi ai =ajb на основании графика рис. 5.16, б может быть построена зависимость y=fi{g), которая изображена на рис. 5.17. а как для положительных, так и для отрицательных значений g. На этом же рисунке штриховой линvleй показана та же статическая характеристика y=fi{g), но при отсутствии флуктуационной помехи. Из рисунка следует, что флуктуационная помеха в системе с ограниченной линейностью подавляет усиление. В точке g=x=0 по наклону

характеристики можно определить, что общий коэффициент передачи двух звеньев составляет примерно 37% от коэффициента передачи при отсутствии флуктуационной помехи и равен 3,7.

На основании графиков, изображенных на рис. 5.16,5, г, может быть построена зависимость среднеквадратичного значения случайной составляющей сигнала на выходе от полезного сигнала на входе при 0.,.=2 В (рис. 5.17, б):

= 7<;t = 0.5c[9i(xi, cti)4-fp2(i.

где Xi=a:/6, ai=a/6.

Случайные процессы в замкнутых нелинейных системах. В замкнутых системах (см. рис. 5.5, а) при использовании статистической лине-аризации возникают трудности, связанные с тем, что сигнал на входе

0д,В 10\-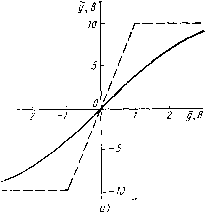

-г -/

2 д,в

Рис. 5.17

нелинейного элемента в канале ошибки зависит от получаемых коэффициентов линеаризации, которые в свою очередь определяются параметрами сигнала. Это приводит к необходимости решать систему уравнений, связывающих эти величины. Рассмотрим задачу анализа нелинейной системы при действии случайного входного сигнала. При этом будем предполагать, что регулярная составляющая исследуемой величины системы (математическое ожидание) постоянна или медленно меняется во времени по сравнению с составляющими основных частот спектра случайной составляющей.

Рассмотрим методику расчета нелинейных замкнутых систем при случайных воздействиях применительно к расчету ошибки. При этом предположим, что нелинейность находится во входных элементах канала управления. Это может быть, например, дискриминатор. Тогда входным сигналом для нелинейности будет ошибка системы управления. В этом случае математическое ожидание х соответствует математическому ожиданию е, а среднеквадратичное значение оОе-