в случае однозначной нeлvшeйнocта расчетная формула npvio6pe-тает Bvw

(x-xf>)b(x)dx-F.

(5.23)

В более общем случае, когда y=F(x, рх), а также при наличии петлевых нелинейных характеристик формула (5.23) оказывается более сложной. Она может быть получена при использовании тех же обобщений, которые были сделаны при нахождении формул (5.20) и (5.21).

Второй способ предполагает определение эквивалентного коэффициента передачи из условия минимума математического oжvlдaния квадрата разности истинного значения f и ее заменяющегося значения (5.18). Это условие имеет вид

отсюда

M{[F-F-q>x>f\ = min, M{W}

7 =

.г Fx. Ох

(5.24) (5.25)

здесь ггх - значетш взаимной коррелящюнной функции переменных F п X при т=0.

Если нелинейная saBvicvmocTb имеет однозначный характер, то из (5.25) vmecM

00 00

= 1 г FOxQ ix)dx = ~ [ F (х+х) xQ (х) dx. (5.26)

01- J Ox J

Эта формула также может быть распространена на случай, когда y=F{x, рх), и на петлевые характеристики по аналогии с формулами (5.20) и (5.21).

Второй способ определения эквивалентного коэффициента передачи приводит к более простым формулам. С точки зрения точности оба метода примерно равноценны. В некоторых случаях первый метод дает завышенные значения для оценки корреляционной функции величины y=F{x), второй - заниженные. Поэтому существует рекомендация [4] использовать для расчета среднее значение двух эквивалентных коэффициентов передачи, определенных двумя способами.

Статистическая линеаризация типовых нелинейностей. Рассмотрим идеальную релейную характеристику (рис. 5.14, а). При положительном значении X в соответствии с формулой (5.19)

ОхГ2п .

U ехр

1 (х-х

2 I 0,

(5.27)

где интеграл вероятностей Ф

Числовые значения интеграла вероятностей имеются в справочниках. Для отрицательных значений х результат получается аналогичным, но с обратным знаком.

Зависимость относительного значения смещения на выходе FIc от относительного значения смещения на входе xlo для нормального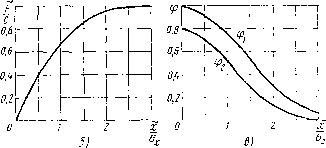

Рис, 5.14

закона распределения входной величины показана на рис. 5.14, б. Характеристика ~F{x) имеет симметрию относительно начала координат (нечетная функция), поэтому случай а:<0 может быть получен из изображенной характеристики инвертированием знаков х п F.

Линеаризация разложением в ряд Тейлора дает из (5.27) эквивалентный коэффициент передачи регулярной составляющей в точке х= =Хо для малых отклонений от этой точки:

- dF

в частном случае при а:о=0

(5.28)

(5.29)

В соответствии с формулой (5.23) эквивалентный коэффициент передачи случайной составляющей

b(x)dx-F = -\ 1-Ф(ха ф(;с,а. (5.30)

В соответствии с формулой (5.25) 2с

У 2я

= ехр

(5.31)

Графики полученных функций ф1 и фа построены на рис. 5.14, в. Эти функции являются четными, т. е. ф1(-х, сГз.)=ф1(л:, а) и -х, а)=Ф2(л:, G).

В частном случае, когда х=0 и F=0, эквивалентный коэффициент передачи из формул (5.30) и (5.31) определяется соответственно выражениями

ql = clG, 1

<о = с/(а,1/2) = 0,8с/а,. / (-2)

Для релейной характеристики с зоной нечувствительности (рис. 5.15, а) математическое ожидание выходной величины можно выразить через интеграл вероятностей. При 0<.х<.Ь

р = .[ф( ф ( ,)].

При х>Ь соответственно

Р = [Ф( ,)-Ф (- ,)]; здесь 1=(6+;с)/а , и~{Ь-х)10х. F

(5.33) (5.34)

F С 0,8

0,8 0,6

0& 0,2

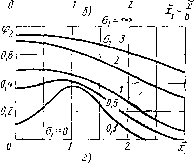Рис. 5.15

Как следует из формулы (5.34), при оо на выходе имеем F с. Полученная характеристика изображена на рис. 5.15, б.

При х<.0 могут быть получены аналогичные формулы. При этом характеристика ~F {х) будет нечетной функцией.