-)та частота соответствует периоду автоколебаний Г = 2яуй = 6,28/25 w 0,25 с. Для нахождения амплитуды автоколебаний определим значение модуля (/со) = = zo(a) в точке пересечения. Модуль частотной передаточной функции линейной части при (o=Q

KTyTf 240-0,016-0,1 gg

Q/l+Qr/l+Qr V + Ta 0,016 + 0,1

Следовательно, Zq (a) = naV(4 Y a-\) = Z,Z. Решение этого уравнения дает два значения относительной амплитуды: а= 1,8 и а = 4,1. В соответствии с рис. 5.10 устойчивому периодическому режиму соответствует пересечение годографа линейной части с нижней ветвью годографа нелинейной части, где амплитуды больше. Поэтому значение а = 4,1 соответствует амплитуде искомых автоколебаний: Л =Ьа = =1-4,1=4,1 угл. мин

Из рис. 5.10 может быть получено условие отсутствия автоколебаний в рассматриваемой системе. Очевидно, что пересечения двух годографов не будет, если при \) = -180° модуль I ил(/ш) < JT/2. В соответствии с изложенным это условие запишем следующим образом:

< я/2.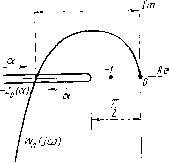

Рис. 5.10

0,6 02

Рис. 5.11

Откуда может быть получено требование к добротности по скорости:

при выполнении которого в системе будут отсутствовать автоколебания. § 5.3. статистическая линеаризация

Основы метода. Исследование прохождения случайных сигналов через нелинейные звенья автоматических систем сопряжено со значительными трудностями и в большинстве случаев не может быть осуществлено точными теоретическими методами. Поэтому в основном для исследования подобных систем нужно использовать моделирование на ЭВМ.

Однако иногда требуется хотя бы ориентировочно оценить влияние нелинейных звеньев при теоретическом анализе системы. В этом случае приобретают значение приближенные методы. Одним из наиболее удобных является метод статистической линеаризации.

При его использовании предполагается, что случайные воздействия на автоматическую систему имеют нормальное распределение. После

прохождения таких воздействий через нелинейные звенья нормальное распределение будет нарушаться. Однако для приближенной оценки точности систе-

Рис. 5.12 мы, как и в случае линейных систем,

можно и здесь воспользоваться двумя первыми вероятностными моментами - математическим ожиданием и дисперсией, что эквивалентно использованию корреляционной теории (или спектральных плотностей).

Сущность статистической линеаризации заключается в том, что нелинейное звено заменяется эквивалентным, которое одинаково с исходным нелинейным звеном преобразует два первых вероятностных момента. При этом предполагается, что, как и в случае гармонической линеаризации, последующие линейные элементы, на которые поступает выходной сигнал нелинейного звена, обладают свойством фильтра и влияние неучитываемых высших вероятностных моментов будет ослаблено. Это и позволяет применить подобный метод для инженерных расчетов.

Разомкнутые системы. Рассмотрим разомкнутую цепь (рис. 5.12), состоящую из линейного звена ЛЗ с передаточной функцией W{p), на входе которого действует случайный сигнал g{t), и нелинейного звена ЯЗ. Выходная величина y{t) связана со входной x{f) нелинейной зависимостью y=F (х).

Пусть входной сигнал g(t) представляет собой сумму математического ожидания g{t), являющегося регулярной функцией времени, и центрированного случайного стационарного процесса g(t), для которого известны корреляционная функция/Cg (х) и спектральная плотность 5(сй).

Сигнал на выходе линейного звена x{t) представим также в виде

суммы регулярной составляющей - математического ожидания x{t) и центрированного случайного процесса x°{t).

Регулярная составляющая на выходе линейного звена определяется обычными методами расчета прохождения детерминированного сигнала через линейную систему (гл. 2).

Для случацной составляющей на выходе линейного звена может быть определена корреляционная функция или спектральная плотность в соответствии с изложенным в гл. 3. Это дает возможность определить дисперсию выходной величины D.

Таким образом, на выходе линейного звена оказываются известными математическое ожидание x{t) и дисперсия Dx-

Величину y=F{x) на выходе нелинейного звена представим также в виде суммы регулярной составляющей (математического ожидания)

Рис. 5.13

И случайной составляющей

f = f+ fo = f+ <7 д; = + <7 л; . (5.18)

Здесь введен эквивалентный коэффициент передачи нелинейного звена (7° по случайной составляющей. При этом регулярную составляющую F можно использовать непосредственно либо представить в виде произведения qx, где q - эквивалентный коэффициент передачи регулярной составляющей. Для определения последнего коэффициента применимы различные методы линеаризации зависимости f=f(A:). Статическая линеаризация дает q= = FIx, а динамическая - q=dF/dx. Последний случай совпадает с обычной линеаризацией, используемой в нелинейных системах и вытекающей из разложения вряд Тейлора.

Регулярная составляющая может быть определена по формуле для математического ожидания. Для однозначной нелинейной функции

F = M{F{x + x)} = 5 F {x + xO)b{x)dx, (5.19)

- 00

где &(л:) - плотность вероятности.

Для нелинейности более общего вида: y=F{x, рх) имеем

со со

Р=] fCx + x\ рх +рх<>){х, px)dxd{px). (5.20)

- 00 - 00

Последняя формула может быть, в частности, использована для определения математического ожидания в случае нелинейных петлеобразных характеристик. Так, для характеристики, изображенной на рис. 5.13, в случае симметричной функции распределения

f= j F{x + xO){}ix)dx + \ j [Fiix + x ) +

-co -bi

+ F,{x + x )] b{x)dx+F{x + x ) (x) dx.

(5.21)

Эквивалентный коэффициент передачи для случайной составляющей можно определить следующими способами.

Первый способ основан на использовании среднеквадратичных отклонений аи Ор. Коэффициент передачи находим по их отнощению:

оо = = 7 / М ((f °)П

(5.22) 165