нейного звена зависит не только от амплитуды, но и от частоты. Если же ограничиться рассмотрением нелинейной зависимости вида г/= =F{x), то процесс нахождения периодического режима можно упростить.

Уравнение (5.16) запишем в виде

л (Н -l/W (а) = -г (а). (5.17)

Последнее уравнение просто решается графически. Для этой цели необходимо построить отдельно АФХ линейной части и обратную АФХ нелинейного звена, взятую с обратным знаком (рис. 5.8, б). Точка пересечения двух АФХ определяет решение уравнения (5.17). Частоту периодического режима cu=Q находим по отметкам частоты на годографе линейной части, а амплитуду а=А - по отметкам амплитуды на годографе нелинейного звена.

Однако найденный периодический режим соответствует автоколебаниям только тогда, когда он будет устойчив в том смысле, что этот режим может существовать в системе неограниченно длительное время. Устойчивость периодического режима можно определить следующим образом.

Предположим, что линейная часть системы в разомкнутом состоянии устойчива или нейтральна. Дадим амплитуде периодического режима некоторое положительное приращение ЛЛ. Это соответствует сдвигу от точки пересечения по годографу нелинейной части в сторону роста амплитуд. Для случая, изображенного, на рис. 5.8, б, это будет сдвиг по годографу гн(й) влево и вниз, что соответствует росту модуля z {a) и уменьшению модуля W {a). В результате произведение W(J(i>)Wji{a) уменьшится по модулю, и АФХ передаточной функции разомкнутой системы (рис. 5.8, а) уже не будет проходить через точку (-1, /0), а пройдет так, что точка не будет охватываться АФХ. Но этот случай соответствует устойчивости замкнутой системы в том смысле, что процессы в ней должны быть затухающими. Поэтому амплитуда колебаний будет уменьшаться.

Таким образом, положительное приращение амплитуды колебаний для случая, изображенного на рис. 5.8, б, влечет за собой переход к затухающему процессу, что вызывает уменьшение амплитуды. Аналогичным образом можно показать, что всякое случайное уменьшение амплитуды колебаний приводит здесь к возникновению неустойчивости замкнутой системы, появлению в ней расходящихся процессов и восстановлению прежней амплитуды колебаний/

Следовательно, всякое случайное отклонение амплитуды колебаний от амплитуды периодического решения А (рис. 5.8, б) так изменяет систему, что амплитуда восстанавливает свое значение. Это соответствует устойчивости периодического режима, который, следовательно, соответствует автоколебаниям.

Критерий устойчивости периодического режима здесь сводится к тому, чтобы часть кривой -гн(а), соответствующая меньшим ампли-гудам, охватывалась АФХ линейной части. Этот случай относится iC виду АФХ системы, который соответствует наличию одной точки

пересечения характеристики с отрицательной частью оси вещественных значений (рис. 5.8, а).

На рис. 5.8, в изображен более сложный случай, когда АФХ разомкнутой системы имеет два пересечения с отрицательной частью оси вещественных значений. Здесь возможно прохождение АФХ через точку (-1, /0) при двух значениях амплитуды: и Ла и соответственно при двух частотах: Qi и Q.

На рис. 5.8, г для этого случая показано взаимное расположение годографов линейной и нелинейной частей системы. Две точки пересечения соответствуют двум возможным периодическим решениям с параметрами Лх и в одной точке и Ла и - в другой. Аналогично тому, как это делалось в проделанном анализе, можно убедиться, что первая точка соответствует неустойчивому периодическому режиму, а вторая - устойчивому, т. е. автоколебаниям.

В более сложных случаях, например при неустойчивой в разомкнутом состоянии линейной части, можно определить устойчивость получаемого периодического режима, рассматривая расположение АФХ разомкнутой системы. Общим здесь остается то положение, что для получения устойчивости периодического режима необходимо, чтобы положительное приращение амплитуды приводило к сходящимся процессам в системе, а отрицательное - к расходящимся.

При отсутствии в системе возможных периодических режимов, близких к гармоническим, что обнаруживается изложенным расчетом, существует много различных вариантов поведения системы. Однако в таких системах, где линейная часть обладает свойством подавления высших гармоник, особенно в таких системах, где при одних параметрах имеется периодическое решение х=А sin Qt, а при других - нет, есть основания полагать, что при отсутствии периодического решения система будет устойчива относительно равновесного состояния. В этом случае устойчивость равновесного состояния можно оценить требованием, чтобы при устойчивой или нейтральной в разомкнутом состоянии линейной части ее АФХ не охватывала годографа -2н(а).

Пример расчета автоколебаний. Рассмотрим релейную следящую систему (рис. 5.9), осуществляющую автоматическое слежение по направлению. Система содержит нелинейное звено нз, представляющее собой чувствительный элемент с релейной характеристикой f (е), где aj и а. - углы поворота задающей и исполнительной осей; 6 = 0,1-02-ошибка (рассогласование) системы, и линейную часть лч, содержащую усилитель, исполнительный двигатель и редуктор. Передаточную функцию линейной части запишем в виде

p(-1-typ)(\-j-tj,p)

где 1 -коэффициент пропорциональности между напряжением на входе усилителя usx и частотой вращения исполнительной оси а, в установившемся режиме-. Ту и Гд - постоянные времени усилителя и двигателя.

Напряжение на вход усилителя поступает от релейного чувствительного элемента в соответствии с зависимостью /вх = /о при еб, ugx=0 при е < b и usx = ~uo при е<-&. Здесь &-зона нечувствительности релейного элемента.

Примем следующие числовые значения: 7у = 0,0]6с, Гд = 0,1 с, ь= 1 угл. мин.

Установившаяся скорость исполнительной оси при подаче напряжения от чувствительного элемента на вход усилителя а2 = 4°/с = 240 угл. мин/с.

Найдем добротность по скорости линейной части с присоединенным коэффициентом передачи нелинейного звена k - Uo/b:

/C = a2/& = i2 = 240c-i.

Частотная передаточная функция линейной части

/м(1 + /мГ,)(1+/мГд)

ffe)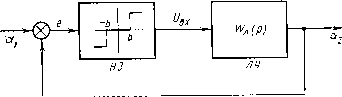

Рис. 5.9

Годограф линейной части изображен на рис. 5.10.

На основании табл. 5.1 (при с= I и Ь=\) нормированное значение коэффициента гармонической линеаризации

где a = o/i> - относительная амплитуда.

Так как для рассматриваемого случая q (а) = 0, то Wy (a)=qo{a), а также

-zo (а) = - 1/Г о (а) - naV(4 ).

Графики изменения до () и Zo (а) в функции относительной амплитуды изображены на рис. 5.1\,а,б. Годограф нелинейной части -Zo (а) изображен на рис. 5.10. Он построен в соответствии с рис. 5.11,5. Годограф имеет две ветви. При а-1 значение -Zj (а) уходит в -оо вдоль вещественной оси.

При увеличении относительной амплитуды модуль величины - Zo (а) уменьшается, при а = 2 достигает минимального значения: zo(a)=n/2, а затем -Zo (а) уходит опять в -оо вдоль оси вещественных значений.

Годограф линейной части может иметь с годографом нелинейной части две точки пересечения. Нижняя из них в соответствии со сформулированным критерием соответствует устойчивому периодическому режиму, т. е. автоколебаниям.

Для нахождения частоты периодического режима необходимо определить, при какой частоте годограф линейной части пересекает отрицательную часть оси вещественных значений. Это будет-Тогда, когда сдвиг фаз, т. е. аргумент комплексной величины Н7д(/сй) достигает значения -180°. Из выражения для (/ш) имеем

tj3 = -90°-arotg сйГу -aratg шГд. Отсюда, полагая cd = Q, имеем

arotg QTy + arotg QTfl = arctg-J-i;- =90°.

Решая последнее равенство, находим угловую частоту автоколебаний: Q=\/}T\T\=\/V 0,016-0,1 =25с-1.