Таблица 5.1

Характеристика нелинейного звена

Идеальная релейная

Релейная

Коэффициенты гармонической линеаризации

Q{a)

4с ка

Релейная

4cb яа2

Релейная

I I о

то b

2сЬ яа

С насыщением

о b

2fe я

6 , 6 i/ , 62

arcsin----I/ 1--5-

a Й r fl2

a S= при a <b)

П родолжение

Характеристика нелинейного звена

Коэффициенты гармонической линеаризации

С ЗОНОЙ нечувствительности и насыщением

2fe(arciSin- - arcsin- +

Идеального дискриминатора

2k л

arosin - - sin 2 arcsin - а 2 \ а

аЬ (k при а < Ь)

Люфта или зазора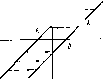

-+.,cs, 1-- +

Здесь коэффициент й=с/& может быть присоединен к передаточной функции линейной части системы; а=а/Ь - относительная амплитуда входного сигнала; lF o(a) - нормированное значение эквивалентной передаточной функции, соответствующее релейной характеристике при Ь=\ и с=1.

В табл. 5.1 приведены результаты гармонической линеаризации для некоторых типовых нелинейностей.

Расчет автоколебаний по критерию Найквиста. Для расчета автоколебаний используют различные критерии устойчивости. Наиболее просто и наглядно использование критерия Найквиста. Этим случаем и ограничимся.

Особенно удобно использование критерия Найквиста в случае, кога имеется нелинейная зависимость вида y=F{x) и эквивалентная передаточная функция нелинейного звена зависит только от амплитуды входного сигнала.

Возмол<ность возникновения в нелинейной системе периодического режима движения определяется появлением в решении характеристического уравнения (5.7) пары часто мнимых корней, когда все остальные корни лежат в левой полуплоскости. Это соответствует прохождению амплитудно-фазовой характеристики разомкнутой системы через точку (-1, /0) комплексной плоскости. Для определения условий прохождения через эту точку приравняем функцию (5.9) -1:

(5.16)

Чтобы решить это уравнение, можно, задаваясь различными значениями амплитуды, строить каждый раз амплитудно-фазовую характеристику. При некотором значении амплитуды а=А характери-

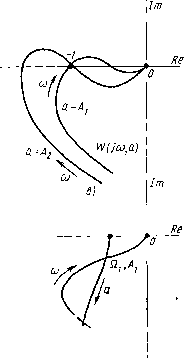Рис. 5.i

стика будет проходить через точку (-1, /0) (рис. 5.8, а). Частота co=Q в точке (-1, jO), определяемая по отметкам частоты на характеристике, и амплитуда а=Л, для которой построена данная характеристика, соответствуют частоте и а.мплитуде искомого периодического режима х=А sin ОЛ.

Замети.м, что подобным образом можно отыскивать периодическое решение для нелинейных зависимостей любого вида, приводящих, в частност!!, к тому, что эквивалентная передаточная функция нели-