в переменной у. Данное предположение носит название гипотезы фильтра. Если это предположение не выполняется и линейная часть представляет собой, например, фильтр верхних частот, то метод гармонической линеаризации может дать ошибочные результаты.

В связи со сказанным будем считать, что на вход нелинейного звена поступает гармонический сигнал х=а sin со/, где а и со - амплитуда и угловая частота. Подставляя это выражение в заданную нелинейную функцию (5.2), разложим ее в ряд Фурье: i/ = F {а sin со = Со +1>1 sin со + С, cos со/ + sin 2сй + CjCOs 2со + ...

Положим, что в искомых колебаниях отсутствует постоянная составляющая, т. е. удовлетворяется равенство

Со = F{asmat)d{at)0. о

Это условие выполняется всегда, когда нелинейная характеристика симметрична относительно начала координат (см. рис. 5.1-5.4) и отсутствует приложенное к нелинейному звену внешнее воздействие.

Можно находить автоколебания и при наличии постоянной составляющей [4], но тогда решение надо искать в виде х=Хо+а sin со.

В записанном разложении в ряд Фурье произведем замену sin со= ==х/а; cos atpx/iaa) и отбросим все высшие гармоники ряда, считая, что они не пропускаются линейной частью. Тогда для нелинейного звена получим приближенную формулу

y = q(a)x + q (а) рх/а, (5.3)

где q(a) и q(a) - коэффициенты гармонической линеаризации, определяемые формулами разложения в ряд Фурье:

= - = -] f (аз!пф)з1пфф, (5.4) о

С 1С

ч = 17 = -\ f (а sin ф) cos ф dtp, (5.5)

где ф=сй/.

Таким образом, нелинейное уравнение (5.2) заменяется приближенным уравнением для первой гармоники (5.3), похожим на линейное уравнение. Особенность его заключается в том, что коэффициенты уравнения зависят от искомой амплитуды автоколебаний. В общем случае при более сложном характере нелинейной зависимости, например y=F(х, х), эти коэффициенты будут функцией как амплитуды, так и частоты искомых колебаний.

Проделанная операция замены нелинейного уравнения приближенным линейным носит название гармонической линеаризации, а коэффициенты, найденные по формулам (5.4) и (5.5), называют гармо-ническилш коэффициентами передачи нелинейного звена.

На основании уравнения линейной части системы (5.1) и приближенного уравнения нелинейного звена (5.3) получаем передаточную функцию разомкнутой системы

и характеристическое уравнение замкнутой системы

Q(p) + R(p}[Q(a)+-p]=0. (5.7)

Из выражения (5.6) подстановкой р-]а находим частотную передаточную функцию разомкнутой системы

) = f{j3[( ) + /V( )]. (5.8)

Ее можно представить в виде произведения частотной передаточной функции линейной части системы 1л(/со), которая является функцией частоты, и эквивалентной передаточной функции нелинейного звена, которая для рассматриваемого типа нелинейной зависимости (5.2) является функцией только амплитуды:

№(/ш, а) = Г,(НГ (а); (5.9)

здесь Г (/ю)=/?(/ю)/(3(/ю); W (a)=q{a}+jq{a).

Модуль эквивалентной передаточной функции нелинейного звена

Г (а) = КЬ(а)Р + [( )? (5.10)

равен отношению амплитуды первой гармоники на его выходе к амплитуде входной величины. Аргумент его

i,(a) = arctg[(a)/(a)] (5.11)

определяет сдвиг фаз между первой гармоникой на выходе нелинейного звена и синусоидальным входным сигналом.

Можно показать, что для нелинейных звеньев с однозначными и симметричными относительно начала координат характеристиками, не имеющими гистерезисных петель, коэффициент гармонической линеаризации q(a)=0. Поэтому для таких звеньев эквивалентная передаточная функция является чисто вещественной - W {a)=q(a) и il)(a)=0.

Часто используется величина, обратная эквивалентной передаточной функции нелинейного звена:

z {a) = l/W ia) = u{a) + jvia), (5.12)

называемая иногда эквивалентным импедансом нелинейного звена. Использование ее удобно при расчете автоколебаний по критерию Найквиста.

Гармоническая линеаризация типовых нелинейностей. В качестве примера рассмотрим релейную характеристику, изображенную на рис. 5.1, в. Так как для этой характеристики q(a)-0, то нужно найти

только коэффициент q{a) в соответствии с формулой (5.4). Для этой цели подадим на вход звена гармоническую функцию и построим изменение во времени выходной величины (рис. 5.7). В пределах зоны нечувствительности \х\<:Ь вы одной сигнал равен нулю. Вне зоны

I ai=cot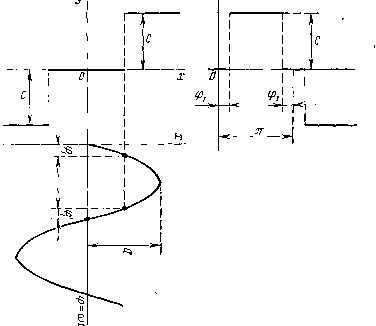

Рис. 5.7

нечувствительности выходной сигнал у=+с. Фазовый угол соответствующий равенству мгновенного значения входного сигнала х=Ь, равен arcsin(&/a). Учитывая симметрию подынтегральной функции, имеем

2я я/2

(а) = -Г F(o:sin ф) sin фйф = - Г csinфdф =

о ф1

Так как (а)=0, то окончательно

() = - ( >)- (5-14)

Иногда в рассмотрение вводят нормированную эквивалентную передаточную функцию. Для этого формулу (5.14) представляют в виде

(a) = F,(a)=i YT=kl ]/ГП: = й о(а). (5.15)