нтаной функции имеет вид

W (/со, t) е = \w{t,V) е dA,. (4.35)

Это выражение представляет собой интегральную связь между комплексным входным сигналом е и комплексным выходным сигналом W{j(d, )е системы с импульсной переходной функцией w{t, Х).

\t-0 Ветестденная часть . 1<, / I I--1 I

sin tot l ..--f~tJX~T--

Генератор ФазодраЩШт ШишЧШЬ Xt[Ct,f)

синусоидальных >

сигналов

Рис. 4.6

Так как реально можно получить только действительные сигналы, необходимо отдельно определить вещественную и мнимую части координатной функции. Вводя обозначения

хДсо, О = Re [W(/со, )е/ ],

x,(co, ) = 1т[Г(/со, Ое ], (4.36)

запишем предыдущую формулу в виде

хДсо, )-1-/л; (со, t)=\w{t, А) (соэсоА-Ь/sincoA,) dA р

X, (со, /) = 5 wXt, Я) cos (соА) dl, Х{ (со, г;) = J да (t, А) sin (соЯ) dX. (4.37) о о

По полученным формулам легко построить схему моделирования, показанную на рис. 4.6. Схема позволяет определить вещественную и мнимую составляющие координатной функции для фиксированных значений частоты. Так как обычно требуется определить дисперсию

+ 00

выходного сигнала, то согласно формуле £>вых(0= \ вх( >)Х

X li(/co, t)\d(i) необходимо иметь квадрат модуля нестационарной параметрической передаточной функции системы. Возводя в квадрат левые и правые части соотношений (4.36) и складывая результаты, получаем

[хДш, ОР+[х,.(ш, t)Y]W{jco, t)\\ (4.38)

Эти формулы используются для определения квадрата модуля параметрической функции на модели. Схема моделирования состоит из двух одинаковых устройств с импульсными переходными функциями

w{t, ), на вход которых одновременно в момент времени -0 подают синусоидальные сигналы со сдвигом по фазе на я/2 один относительно другого. Выходные сигналы возводят в квадрат и складывают (рис. 4.7). Повторно проводя эксперимент для различных значений

sin Mt

Рис. 4.7

частоты, можно получить серию кривых, из которых построением легко найти \W{ja, для данного момента наблюдения / (рис. 4.8). Эта функция используется для вычисления D).

Этот способ также не обеспечивает полной автоматизации процесса определения дисперсии, так как требуется выполнить операцию интегрирования по переменной со. Однако,общий объем работы значительно сокращается по сравнению с предыдущим способом, определение же интеграла сводится к подсчету площади, образуемой кривой Sia)\Wija, 01 с осью (О.

Моделирование нестационарных процессов. В большинстве случаев оно основывается на непосредственном использовании формул,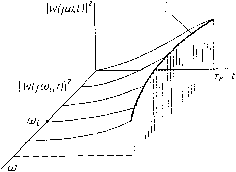

Рис. 4.8

связывающих корреляционную функцию входного и дисперсию выходного сигнала:

вык(0 =

X(u, l)du

H{t, l)=\wit, u)RAu, l)du.

(4.39)

Так как во всех этих формулах интегрирование ведется по второму аргументу импульсной переходной функции, то для использования моделирующих устройств необходимо иметь сопряженную импульс-

иую функцию, т. е. функцию w(t, ), у которой независимой переменной является , а t играет роль параметра. Для этого достаточно найти дифференциальное уравнение с независимой переменной , которому бы удовлетворяла функция с фиксированным значением t. Этому условию отвечает сопряженное уравнение. Следовательно, моделируя сопряженное уравнение для некоторого фиксированного значения t, можно получить выходной сигнал в виде w(i, ) как функцию . Однако моделирование сопряженных уравнений в ряде случаев вызывает затруднения и неудобства, в особенности, если система задана структурной схемой. Разработана методика применения моделирующих устройств для исследования систем в общем нестационарном случае, основанная на построении специальных схем моделирования, позволяющих полностью автоматизировать весь процесс вычисления дисперсий. Теория пострбения указанных схем, называемых инверсными, является развитием идеи сопряженных систем в применении к преобразованию структурных схем. Эта теория состоит в отыскании правил преобразования структурных схем исследуемых систем таким образом, чтобы реакции их на входной импульсный сигнал в виде дельта-функции были эквивалентны изменению соответствующей импульсной переходной функции w{t, ) по переменной при некотором фиксированном значении t. Аналитически это выражается в том, что необходимо найти дифференциальные уравнения звеньев и уравнения связей между ними с независимой переменной I, которым бы удовлетворяла функция w{t, ), одновременно удовлетворяющая исходным дифференциальным уравнениям звеньев и уравнениям связей с независимой переменной t.

Глава 5

НЕЛИНЕЙНЫЕ СИСТЕМЫ § 5.1. ОСНОВНЫЕ ПО.НЯТИЯ

Виды нелинейных систем. Нелинейной называют систему, описываемую нелинейным дифференциальным уравнением. Обычно система является нелинейной вследствие наличия в ней одного или нескольких звеньев, описываемых нелинейным дифференциальным уравнением или имеющим нелинейную статическую характеристику. При этом система может иметь в своем составе линейные или линеаризованные обычными методами звенья.

Нелинейным считают такое звено, которое не поддается линеаризации в том смысле, что отказ от учета его нелинейных свойств существенно искажает результаты последующего анализа и делает их неприемлемыми.

Нелинейные звенья могут входить в состав автоматической системы вследствие неизбежности применения тех или иных технических устройств, но могут быть случаи, когда нелинейные зависимости специально вводятся в систему для получения каких-либо желаемых ее свойств.

е* Зак. 501 147