момента приложения единичного импульса на входе системы (0= =const). Эту функцию называют нормальной весовой функцией системы с переменными параметрами:

w = w{t - b, Ь), д = const. (4.4)

Она является параметрической функцией, так как в нее входит фиксированный параметр d=const и ее можно использовать для характеристики переходных процессов в нестационарной системе.

u/lt-if,<>}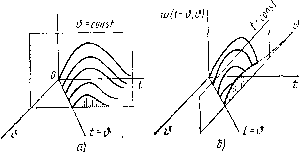

Рис. 4.2

Сечение поверхности весовой функции вертикальной плоскостью, параллельной оси Од, дает так называемую сопряженную функцию веса (рис. 4.2, б): w=w{t-b, Ь), =const. Она может быть получена путем обработки семейства нормальных весовых функций, построенных для различных моментов приложения единичного входного импульса (рис. 4.3). Эта функция также является параметрической, так как содержит параметр =const.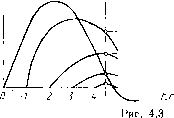

0 1

3 4 i),C

Сопряженная функция является функцией смещения но может быть представлена и как функция 9=-0 (рис. 4.2, б), называемого реверССмешением, так как 9 отсчитывают от точки b-t в сторону, противоположную смещению д.. Это осуществляется подстановкой в сопряженную весовую функцию значения b=t-9 при ==const:

w = w{Qf t~Q), = const.

Проиллюстрируем сказанное примером. Пусть имеется весовая функция нестационарной системы вида: w{t-b, b)=k&~*~Vt. Зафиксировав смещение и положив &=Oo=const, получаем нормаль-

ную функцию веса: w(t-bo, &o)=e *e- V, или в другом виде, при переходе к аргументу x=t-Ь:

Нормальная функция веса показана на рис. 4.4, а, б. Зафиксировав текущее время и положив /=/o=const, получим сопряженную функцию веса (рис. 4.4, б):

Перейдя к реверс-смещению Q=U-получим ш(9, i - Q) = ke-/to.

Эта функция построена на рис. 4.4, г. Весовая функция является характеристикой линейной нестационарной системы. Ее сечение (см. рис. 4.2, а), т. е. нормальная весовая функция, построенная для раз-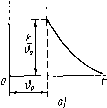

1> =consr -4-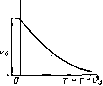

л = const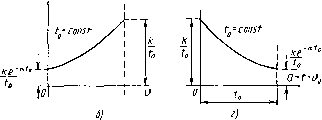

Рис. 4.4

личных значений смещения ОдТ, где Т - время работы системы, может быть использована для оценки качества регулирования (колебательности, быстроты затухания процессов и т. д.). Второе ее сеченне (см. рис. 4.2, б), т. е. сопряженная весовая функция, может быть использована для нахождения реакции системы на входное воздействие произвольного вида. Пусть на систему с весовой функцией w{t-Ь, Ь) действует входной сигнал f{t). Элементарная реакция системы на импульс, приложенный в момент времени Ь, может быть найдена как произведение площади импульса f{t)dQ на весовую функцию, которая

является реакцией системы на импульс единичной площади:

dx(t) = w{t - , 0) при tQ. (4.5)

Полный сигнал на выходе системы x{t) определяем как сумму элементарных реакций вида (4.5):

x{t)=[w{i-Q, d)/(d)dd. (4.6)

Интегрирование ведем по смещению О. Весовая функция является сопряженной. Верхний предел интегрирования можно заменить на бесконечность, так как при Q>-t весовая функция тождественно равна нулю:

x{t)=lw{t - Q, d)/(d)d&. о

При переходе к реверс-смещению формула (4.6) может быть представлена в виде интеграла свертки:

x{t)=lw{e, t-e)f{t-e)dQ. (4.7)

Построение переходных процессов. Нахождение переходной функции или функции веса нестационарной системы, являющейся ее исчерпывающей характеристикой, обычно сопряжено с большими трудностями. Существующие методы позволяют решать задачу нахождения весовой функции только в численном виде. Однако для систем регулирования, описываемых дифференциальными уравнениями первого и иногда второго порядков, удается решать задачу в общем виде. Поэтому в некоторых случаях приходится сложную нестационарную систему приближенно сводить к более простой, которая описывается уравнением не выше второго порядка. Большинство нестационарных систем относится к так называемым квазистационарным системам, параметры которых меняются сравнительно медленно. В таких системах коэффициенты дифференциального уравнения мало меняются в течение времени переходного процесса, определяемого временем затухания нормальной функции веса.

Дифференциальное уравнение первого порядка dx/dt+P{t)x=Q{t) имеет аналитическое решение:

x(/) = e-S(o[5 Q(/)eS{0 + c], (4.8)

где S{t)=iP{t)dt; С - постоянная интегрирования, определяемая начальными условиями.

Пример 4.1. Пусть имеется уравнение

t+aix = f. (4.9)

Определяем для него семейство переходных характеристик

9(-0, 0) = <?(т, О).