/Для минимизации продифференцируем последнее выражение по /Сг и приравняем производную нулю:

Решая последнее уравнение, находим

/С?Р = (4Di, /yV )2/5 = (4.4/1,25)2/5 = 2,77 с.

Минимальное значение, дисперсии полной ошибки

Подставляя исходные значения в последнюю формулу, получаем Df = А 4.4-1,25* = 2,6м

Минимальное среднеквадратичное значение ошибки сопровождения по дальности

ff =kdf = 1.61м.

Заметим, что ошибка при применении двух интеграторов оказалась меньше, чем в случае использования одного интегратора.

Постоянная времени параллельной цепи (см. рис. 3.12) должна

быть принята

т= l/l C Pt = (1/2,773)-! 0,6 с.

Условие устойчивости т>Тв (0,6 с>0,01 с) выполняется.

Области применения одного или двух интеграторов в цепях сглаживания. Полученные выражения для минимальных дисперсий ошибок сопровождения по дальности позволяют установить границы целесообразности введения в систему одного или двух интеграторов. Для этого приравняем полученные значения Df :

Из последнего выражения находим граничные значения дисперсии и среднеквадратичной величины ускорения объекта:

DI = 0,565 у(ЩЩ, 4 = -j/d. (3.46)

Если заданное значение (Т>а, то следует использовать схему с одним интегратором, а если заданное значение ст<(Т, то преимущество имеет схема с двумя интеграторами.

Подставляя в (3.46) числовые значения, находим

=0,565 25005/1,252 =1,78 105м/с*,

=1/ 1,78-10 = 4,2Ы02м/с2==421 м/с

Так как в нашем примере получилось ст>ст =2 м/с?, то надлежит применять схему с двумя интеграторами.

Глава 4

НЕСТАЦИОНАРНЫЕ СИСТЕМЫ

§ 4.1. МЕТОДЫ ИССЛЕДОВАНИЯ ДЕТЕРМИНИРОВАННЫХ ПРОЦЕССОВ

Общие сведения. Реальные системы радиоавтоматикп, как правило, имеют переменные во времени параметры. Таковы, например, системы радиоуправления подвижными объектами, системы радионавигации и др. Эти системы при работе в различных практических ситуациях содержат одно или несколько звеньев с переменным коэффициентом передачи, зависящим от времени. Так, в системе углового сопровождения вследствие изменения дальности до объекта сопровождения крутизна дискриминатора становится функцией времени.

Для изучения нестационарных систем существует ряд аналитических методов, однако анализ нестационарных систем или систем с переменными параметрами значительно сложнее, чем стационарных. Систему радиоавтоматики называют стационарной, если ее реакция на любое данное возмущение не зависит от момента его приложения, т. е. при любом сдвиге во времени входного возмущения без изменения его формы выходная переменная в стационарной системе претерпевает такой же сдвиг во времени без изменения своей формы. В нестационарных системах при сдвиге входного возмущения во времени без изменения формы их выходные переменные сдвигаются во времени и изменяют свою форму.

Математически это выражается в том, что дифференциальные уравнения системы содержат переменные во времени коэффициенты. Непостоянство коэффициентов уравнения возникает вследствие изменения во времени параметров отдельных звеньев. Изменение коэффициентов во времени усложняет задачу исследования динамики подобных систем. Только дифференциальные уравнения с переменными параметрами первого и второго порядков могут быть решены в общем виде. Уравнения более высоких порядков решаются методами численного интегрирования, а также на ЭВМ [4].

Синтез систем радиоавтоматики с переменными параметрами осуществляется с помощью ЭВМ, которая позволяет оценить качественные показатели и подобрать необходимые корректирующие средства. Синтез нестационарных систем с переменными параметрами резко упрощается, если систему рассматривать как квазистационарную, т. е. такую, параметры которой изменяются настолько медленно по сравнению с длительностью переходных процессов, что их можно считать постоянными [4]. Таким образом, нестационарная система описывается уравнением

= о(0+ -\-b -At)-\-bAt)f{t)- (4.1)

Коэффициенты о, . . . , а и &о, . , &т являются функциями времени, которые задаются либо графиками, построенными на основании эксперимента, либо аналитически.

Переходная функция и функция веса. Так как коэффициенты уравнения (4.1) меняются с течением времени, то эти функции будут зависеть от момента приложения единичного скачка или единичного импульса на входе.

На рис. 4.1 показаны графики изменения во времени одного из коэффициентов исходного уравнения ai{t), переходной функции q и функции веса w. При поступлении на вход нестационарной системы

единичной ступенчатой функции f(t) = l{t-) реакция ее, представляющая собой переходную функцию данной системы q{t-Q, )=q{t, Ь), оказывается зависящей от двух переменных: текущего времейц t, отсчитываемого от некоторого момента, соответствующего, например, началу работы системы, и времени & (смещения), соответствующего поступлению на вход ступенчатой функции. Ее можно также представить в виде функции смещения & и текущего времени т=/-{}, отсчитываемого от момента приложения ступенчатой функции на входе.

Если на вход подать единичную импульсную функцию, которую можно представить как предел отношения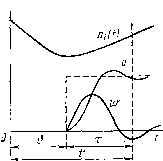

Рис. 4.1

б ( ) = Иш (-)-Ш-(04-А0)] J

(4.2)

то процесс на выходе, т. е. функцию веса, по принципу суперпозиции, можно представить в виде разности двух смещенных на аЬ переходных функций с измененным в 1/Д-& раз масштабом:

w{t-

Правая часть этого выражения - производная от переходной функции по аргументу О с обратным знаком. В результате получим формулу, связывающую функцию веса системы с переходной функцией

(4.3)

Весовая функция оказывается зависящей от тех же переменных: t или j и . Ее можно изобразить в виде некоторой поверхности (рис. 4.2). Эта поверхность переходит в плоскость при t<. Границе перехода поверхности в плоскость соответствует биссектриса t=Q. Это объясняется тем, что в реальных системах реакция не может появиться ранее, чем будет приложен импульс на входе системы [4]. Поэтому при t< функция веса должна быть тождественно равна нулю. Сечение поверхности весовой функции вертикальной плоскостью, параллельной оси t (рис. 4.2, а), дает весовую функцию для зафиксированного