и коэффициенты передачи kj звеньев пересчитывают в машинные параметры TI и kj в соответствии с соотношениями:

( rtifk,- -для дифференцирующих звеньев,

kj =\ - для позиционных звеньев,

Kmjkj - для интегрирующих звеньев. К*г = КгЩ - для добротности системы с астатизмом г-го порядка.

Соответственно единица измерения машинного времени (машинная секунда) i=mlc, т. е. скорость протекания процессов в модели уменьшается в trit раз по сравнению по скоростью протекания процессов в моделируемой системе.

Набор задачи на электронной модели структурного типа может быть осуществлен двумя способами: 1) по дифференциальному уравнению исследуемой системы; 2) по структурной схеме исследуемой системы [5].

Рассмотрим моделирование системы по ее дифференциальному уравнению. Для определенности рассмотрим систему АСН, описываемую дифференциальным уравнением третьего порядка (1.6), которое запишем в виде

(аор + а,р + а,р + a,)y{t) b,g (t). (2.38)

Переходя к машинным переменным Ui=mg и U2=my, получим дифференциальное уравнение модели исследуемой системы

а,и, + а,и, + а,1/, + сци,Ь,и (2.39)

которое с точностью до обозначений входной и выходной переменных совпадает с уравнением исследуемой системы.

Для составления семы набора уравнения (2.39) на модели разрешим это уравнение относительно старшей производной:

(2.40)

P = V o; Щ = а/ао, k=l, 2, 3.

Рассмотрим цепочку из трех последовательно соединенных интеграторов (рис. 2.18). Если на вход первого интегратора подать величину и2, то на выходе интеграторов получим соответственно (с учетом того, что каждый операционный усилитель изменяет знак напряжения)

Просуммировав эти величины и входну ю величину с соответст-вующи.ми коэффициентами, получим на выходе сумматора величину, определяемую правой частью выражения (2.40), т. е. величину U2, которая поступает на вход первого интегр атора. Таким образом, будет получена схема набора дифференциального уравнения (2.38), представленная на рис. 2.18.

Подавая на вход модели напряжение Ui(t) = Uol (t), получим на выходе напряжение Uiit), воспроизводящее переходную характеристику исследуемой системы.

Преимуществом рассмотренного метода моделирования автоматических систем является сравнительная простота схемы набора на модели дифференциального уравнения, в которой используются усилители, выполняющие простейшие типовые операции - интеграторы, инверторы и сумматоры.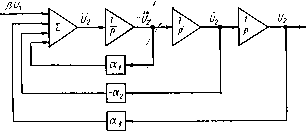

Рис. 2.18

Недостатком метода является невозможность исследования влияния отдельных параметров системы на ее динамические характеристики, что обусловлено тем, что каждый коэффициент дифференциального уравнения системы зависит от нескольких ее параметров, а не от одного.

В этом отношении более удобным является метод моделирования системы по ее структурной схеме. При использовании этого метода составляют модели звеньев исследуемой системы, затем модели звеньев соединяют между собой в соответствии со структурной схемойсистемы и замыкают цепь главной обратной связи. При этом первый (входной) операционный усилитель модели всегда является сумматором с двумя входами: один для машинного управляйщего воздействия Ui(t) и второй для машинного сигнала обратной связи Uit).

Поскольку обратная связь должна быть отрицательной, то, если в контуре модели системы содержится нечетное число последовательно соединенных операционных усилителей, выходное напряжение модели подводится непосредственно к первому операционному усилителю модели, в противном случае - через инвертирующий усилитель с коэффициентом передачи к=-\.

Рассмотрим составление схемы набора системы АСН при моделировании ее по структурной схеме. Уравнение (1.6) этой системы получено из совокупности уравнений (а)-(д) (см. § 1.3), на основании которых напишем передаточные функции функциональных элементов этой системы.

Передаточная функция дискриминатора др(р)=др соответствует безынерционному звену.

Передаточная функция усилителя Wy{p)=kyl{\ + Typ) соответствует апериодическому звену первого порядка.

Передаточная функция объекта управления двигателя с редуктором и следящей антенной

исполнительного

Woy (Р) =

P{i + T p)

(2.41)

соответствует инерционному интегрирующему звену.

Для упрощения схемы набора объединим звенья, соответствующие дискриминатору и усилителю, в одно звено с передаточной функцией:

ь ь

ду КР) - 1 +

(2.42)

Тогда структурная схема рассматриваемой системы может быть представлена в виде последовательного соединения двух динамических

Pit]

кдр ку

Рис. 2.19

звеньев: апериодического звена первого порядка с передаточной функцией (2.42) и инерционного интегрирующего звена с передаточной функцией (2.41), как показано на рис. 2.19.

Передаточная функция разомкнутого контура этой системы

W ip)=(,) W, ip) w, ip)= ;;:;;(f;,,)=.(i-frnV-br,.)

(2.43)

Составив в соответствии с табл. 2.1 схемы набора на модели указанных звеньев и соединив их в соответствии со схемой рис. 2.19, получим

1 iC

Рис. 2.20

схему набора исследуемой системы, представленную на рис. 2.20. В состав модели включен делитель напряжения с регулируемым коэффициентам передачи k-l для регулировки коэффициента передачи К1 модели.

Передаточная функция W*{p) разомкнутого контура модели системы АСН, соответствующая схеме рис. 2.20:

U-z (Р) . К1

Ueip) р{Х + Т1р)(\+Т;р)