матики является эффективным средством повышения помехоустойчивости этой системы.

Заметим также, что, как следует из (2.33), система автоматического сопровождения движущихся объектов с астатизмом второго порядка обеспечивает измерение не только текущих координат объекта, но и скорости его движения.

Установившаяся ошибка при гармоническом воздействии. В задачах анализа и синтеза систем радиоавтоматики широко используются

частотные методы и, в частности, метод логарифмических частотных характеристик. В этом случае оказывается полезной оценка установившейся ошибки системы при гармоническом воздействии.

Запишем гармоническое задающее воздействие с частотой сй в комплексной форме: g{t)=gM ехр(/ХО. где -комплексная амплитуда, учитывающая начальную фазу колебания g{t). Тогда установившаяся ошибка системы e{t) будет представлять собой также гармоническое колебание с амплитудой бм и частотой со : е()=ем ехр (faj). По аналогии с (1.32) для отношения комплексных амплитуд ошибки и задающего воздействия получим eJgu=He{}(i)J, где Яе(/со) = 1/[1--+ W{j(ji)] - частотная передаточная функция системы для ошибки по задающему воздействию.

Оценивая точность системы при гармоническом задающем воздействии по амплитуде ошибки, в соответствии с (1.37) получим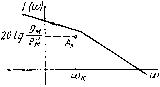

Рис. 2.14

I I + W(/M,)

(2.34)

так как амплитуда ошибки должна быть значительно меньше амплитуды задающего воздействия, что возможно, как следует из приведенного выражения, лишь при \W{jajll.

На основании (2.34) можно сформулировать требования к ЛАХ из условия, чтобы амплитуда ошибки не превышала заданного допустимого значения eJ, при заданной частоте со задающего воздействия. Из (2.34) при вме получаем А (сй)>м/е°, откуда находим условие для ЛАХ:

L(coJ = 201g(coJ>201gf. (2.35)

Таким образом, для выполнения приведенного условия точности ЛАХ системы должна проходить не ниже контрольной точки Л с координатами (й , L(aJ, как показано на рис. 2.14.

§ 2.4. ИСПОЛЬЗОВАНИЕ ЭЛЕКТРОННЫХ ВЫЧИСЛИТЕЛЬНЫХ МАШИН

Общие сведения. При исследовании систем радиоавтоматики, особенно описываемых дифференциальными уравнениями высокого порядка, а также уравнениями с переменными коэффициентами и нели-

нейными уравнениями, широкое применение находят электронные вычислительные машины, как аналоговые (АВМ), так и цифровые (ЦВМ).

Применение вычислительных машин позволяет исследовать процессы в системах в тех случаях, когда нахождение решения дифференциального уравнения системы аналитическими методами затруднительно или вообще невозможно. Исследование систем радиоавтоматики посредством вычислительных машин называют моделированием этих систем - аналоговым или цифровым, в зависимости от типа вычислительной машины.

\Моделирование систем радиоавтоматики на АВМ. Аналоговое моделирование динамических систем и, в частности, систем радиоавтоматики основано на том, что процессы в аналоговых вычислительных машинах описываются дифференциальными уравнениями. Причем схему модели на АВМ можно составить так, что дифференциальное уравнение модели будет таким же, как и дифференциальное уравнение исследуемой системы. Тогда изменения во времени выходной величины модели будут характеризовать соответствующие изменения выходной величины системы.

Существует две разновидности электронных моделирующих машин: модели структурного типа и модели матричного типа. Первые позволяют моделировать исследуемую систему по ее дифференциальному уравнению, записанному в обычном виде, или по ее структурной схеме, что дает возможность достаточно просто исследовать влияние параметров системы на ее динамические характеристики. Модели матричного типа требуют записи дифференциальных уравнений исследуемой системы в особой матричной форме и потому менее удобны для исследования замкнутых автоматических систем.

В дальнейшем рассмотрим лишь модели структурного типа.

Основным элементом аналоговой вычислительной машины является операционный усилитель, представляющий собой усилитель постоянного тока с большим коэффициентом усиления по напряжению (порядка 10*-10). Во входную цепь операционного усилителя включается некоторое сопротивление Zi{p), и кроме того, усилитель охватывается отрицательной обратной связью через сопротивление Zo{p), как показано на рис. 2.15. При этом передаточная функция операционного усилителя выражается через сопротивления Zi{p) и Zi,{p):

Знак минус в (2.36) показывает, что операционный усилитель инвертирует входной сигнал (меняет его знак). Это связано с установкой в усилителе нечетного числа каскадов.

Если во входную цепь операционного усилителя включить резисторы Ri, Ri, . . ., Rn, а в цепь обратной связи сопротивление Ro, как показано на рис. 2.16, то получим суммирующий усилитель, выходное напряжение которого

А= 1 *

или при

Ri - - Rn - R

2 (p) = 2 (P). где = - RJR.

Включая BO входную цепь и в цепь обратной связи операционного усилителя различные комплексные сопротивления, получим, как следует из (2.36), усилители с различными передаточными функциями.

z.ipi u o-q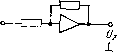

и, ZM

Рис. 2.15

Рис. 2.16

Это дает возможность моделировать динамические звенья автоматических систем. Схемы набора на аналоговой модели типовых звеньев приведены в табл. 2.1, в соответствии с которыми могут быть найдены соответствующие передаточные функции.

1. Безынерционное звено. На основании (2.36) имеем

W{p) = k, где k==-RJR,.

2. Идеальное интегрирующее звено. В соответствии с (2.36) находим

W{p)-XclRklp, где k = -\/(RC).

3. Апериодическое звено первого порядка. Имеем Zi{p)=Ri, Zo{p)~ =RJ{l~{-R2Cp). На основании (2.36) получаем

Wip)=k/il+Tp), где k = ~R,/Ri, T=.Rfi.

4. Инерционное дифференцирующее звено. Имеем Zq(p)=Ro, Zi{p)= = R.i + \/Cp=(l+RiCp)/Cp. В соответствии с (2.36) получаем

W{p)kp/il + Tp), где k=-RjO, T = R,C.

5. Изодромное звено. Имеем Zoip)=(l+RoCp)ICp, Zi{p)=Ri и в соответствии с (2.36) получаем

W{p)k(\ + Tp)/p, где k-MRfi, T = R,C.

В некоторых АВМ (например, в машине МН-10) отсутствует возможность включения последовательной RC-цет в цепь обратной связи операционных усилителей. В этом случае изодромное звено набирают на модели в соответствии с его определением как параллельного соединения идеального интегрирующего и безынерционного звеньев по схеме рис. 2.17, для которой

W (п\--\ L-ji -ь л, - ь + Тр