того контура системы с астатизмом второго порядка

Q(p)pllii + T,p)

имеет два корня, равных нулю, и п-2 корней с отрицательной вещественной частью. Применяя критерий Михайлова к этому полиному, находим, что при изменении со от-оо до оо полное приращение аргумента этого полинома Аг[)д=(/г-2)я.

Тогда Аг[)1=Аг[)д-Аг[)д=/гя-{п-2)я=2я. Это означает, что вектор при изменении w от О до оо и далее от -оо до О должен повернуться на угол 2я против часовой стрелки {М- положительно), как показано на рис. 2.5. Из рисунка видно, что АФХ рассматриваемой системы делит плоскость на две области - внутреннюю , лежащую справа от АФХ при движении по ней в направлении возрастания частоты, и внешнюю . Таким образом, как и в предыдущих случаях, система с астатизмом второго порядка будет устойчивой, если точка с координатами (-1, / 0) не попадет во внутреннюю область, т. е. если АФХ разомкнутого контура системы не охватывает эту точку.

Преимуществом критерия Найквиста является возможность использования его для определения устойчивости системы по снятым экспериментально частотным характеристикам, когда ввиду сложности исследуемой системы трудно получить ее дифференциальное уравнение.

Абсолютно устойчивые и условно устойчивые системы. Рассмот-ри.м замкнутую систему радиоавтоматики, описываемую, например,

уравнением (1.6) и имеющую передаточную функцию разомкнутого контура вида

соответствующую астатизму первого порядка. Из (2.12) при р=]а> получаем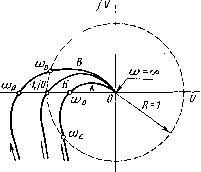

Л ( ) -

Рис. 2.6

г[)(и) = -Y - arctg ©Tj-arctgwTa.

(2.13)

АФХ устойчивой системы, соответствующая (2.12), изображена на рис. 2.6, кривая А (для положительных w). Точка пересечения АФХ с отрицательной полуосью абцисс соответствует частоте сОр, при которой г[)(к1р) = 180°. Точка пересечения АФХ с окружностью единичного радиуса соответствует частоте w, при которой А (Wc) = l. Эту частоту называют частотой среза разомкнутой системы.

Изменению w от О до оо соответствует движение точки по АФХ в направлении, указанном на рис. 2.6 стрелкой. Для устойчивой системы, как следует из рисунка, Wp>Wc.

При увеличении добротности системы Ки как видно из (2.13), АФХ раздувается и приближается к критической точке (-1; / 0), при этом частоты со и сор сближаются и в случае, когда АФХ (кривая Б на рис. 2.6) проходит через критическую точку (-1, /0), становятся равными (со=сор). При этом у характеристического уравнения (2.3) системы появляется пара чисто мнимых корней /Oi,2=±/Pi2 и в системе возникают незатухающие гармонические колебания с круговой частотой Pi2.

Этот случай соответствует так называемой колебательной границе устойчивости. При дальнейшем увеличении добротности Ki АФХ системыбудет охватывать критическую точку (-1, /0) и система станет неустойчивой. Аналогичный результат (2.5) был получен для рассматриваемой системы при использовании критерия Гурвица.

Системы, добротность которых ограничена условиями устойчивости лишь сверху, называют абсолютно устойчивыми системами. При проектировании замкнутых автоматических систем добротность их выбирают не из условий устойчивости, а из условий точности (§ 2.3), и, как правило, добротность систем высокой точности значительно превосходит значение, допустимое по условиям устойчивости. Для обеспечения устойчивости системы в этом случае в ее состав включают корректирующие устройства, содержащие форсирующие звенья, которые в определенной полосе частот уменьшают отрицательный фазовый сдвиг, вносимый интегрирующими и апериодическими звеньями. При этом АФХ деформируется (рис. 2.7, кривая 2). Кривая / соответствует АФХ системы без корректирующих звеньев.

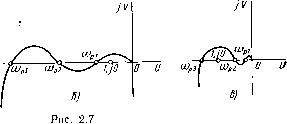Как видно из рис. 2.7, а, АФХ скорректированной системы не охватывает критическую точку (-1, /0), и, следовательно, система устойчива.

Заметим, что после коррекции в системе появилось три частоты (flpi, сор2 и сорз, для которых г()(сор)=-180°, вместо одной со* до коррекции, причем сор1>сор2>сорз. Кроме того, изменились соотношения: сОр<со* -до коррекции, что свидетельствует о неустойчивости системы, и С0р1>с0с - после коррекции, что характерно для устойчивой системы. При этом существенным является то обстоятельство, что две частоты: сор2 и сорз меньше частоты среза сО;..

Рассмотрим устойчивость скорректированной системы. Из рис. 2.7 видно, что при увеличении добротности скорректированной системы точка, соответствующая частоте copi, приближается к критической точ-

Рис. 2.8

ке (-1, /0), и при некотором значении добротности АФХ скорректированной системы будет охватывать критическую точку, как показано на рис. 2.7, б, т. е. система станет неустойчивой. Таким образом, у скорректированной системы ограничение сверху для добротности Ki сохраняется, хотя граничное значение добротности скорректированной

системы в десятки раз больше граничного значения добротности нескорректированной системы.

При уменьшении добротности к критической точке (-1, /0) будет приближаться точка АФХ, соответ-ствующая частоте сорз, как это сле-cpSa о) дует из рис. 2.7, а. При некотором достаточно малом значении Ki эта точка окажется правее точки (-1, /0), и АФХ системы, как видно из рис. 2.7, в, снова будет охватывать критическую точку, т. е. система станет неустойчивой. Следовательно, для рассматриваемой скорректированной системы помимо ограничения добротности сверху появляется ограничение допустимого значения добротности снизу т. е. система будет устойчивой при Ki, если Ктш KiKmax-

Системы, допустимые значения добротности которых имеют ограничение как сверху, так и снизу, называют условно устойчивыми. Заметим, что для условно устойчивых систем с астатизмом не выше второго порядка число частот cOpj, меньших частоты среза, всегда четно. Это используют для анализа устойчивости автоматических систем методом логарифмических частотных характеристик.

На рис. 2.8 представлены ЛАХ и ЛФХ условно устойчивой системы. Как показано на рисунке, для удобства анализа разметка шкалы ЛФХ сделана так, что горизонталь, проходящая через точку ijj=-180°, совпадает с осью частот. Как видно на рис. 2.8, рассматриваемая система имеет три частоты, на которых ф(сйр)=:-180°: и сора и сорз, причем две из них (четное число!) меньше частоты среза со.. При этом, как показано на рисунке, асимптота ЛАХ в окрестности частоты среза имеет наклон -20 дБ/дек.

Можно показать [5], что необходимым и достаточным условием устойчивости системы, состоящей из минимально-фазовых звеньев, является то, что ЛАХ системы в окрестности частоты среза должна иметь наклон -20 дБ/дек или, другими словами, что асимптота ЛАХ, пересекающая ось частот, должна иметь наклон -20 дБ/дек.

При увеличении или уменьшении добротности системы Ki логарифмическая амплитудная характеристика перемещается вдоль оси ординат параллельно самой себе вверх или вниз. При этом точка, соответствующая частоте среза, перемещается по оси частот или вправо (при увеличении Ki) или влево (при уменьшении Ki). Если изменения добротности достаточно велики, то, как показано на рис. 2.8 {ЛАХ-2 яля ЛАХ-3), наклон ЛАХ в окрестности частоты среза уже не будет ра-