Аналогичный результат может быть получен и при наличии среди корней характеристического уравнения комплексно-сопряженных корней.

Сформулируем критерий устойчивости Михайлова. Характеристический полином (2.6) не будет иметь корней в правой полуплоскости, если полное приращение аргумента г) (ш) при изменении ш от -схз до оо равно 2т/2, где п - степень полинома D{p).

Критерий устойчивости Найквиста. Критерий устойчивости Найк-виста позволяет судить об устойчивости замкнутой автоматической cHCTeivbf по виду амплитудно-фазовой характеристики (АФХ) разомкнутого контура этой системы. Вывод критерия Найквиста базируется на критерии устойчивости Михайлова.

Пусть замкнутая автоматическая система описывается дифференциальным уравнением D (р)у (t)=R {p)g{t), где D (р)=аор +ар ~+... +a jp+a - характеристический полином замкнутой системы степени п; R{p)=bop+bip-\-. . +bfn-iP+bjn - полином степени т, причем т<п.

Тогда передаточная функция замкнутой автоматической системы

Р> D(p) a pnjaip -+...a p + a,r

а передаточная функция разомкнутого контура этой системы

1-Н(р) D{p)-R{p) Q(p) CoP + Cip -i-f...+c

где Q{p) - полином степени п.

Введем вспомогательную функцию

Wi(p) = l + W(p)=l-f§j = i. (2.8)

Если

W{ja) = Uia) + jV{a (2.9)

W, (/(О) = 1 + t/ (ш) + jV (ш). (2.10)

Из (2.9) и (2.10) видно, что если начало вектора Wi{ja) поместить в точку с координатами (-1; /0), как показано на рис. 2.2, то конец этого вектора при изменении со от -оо до оо опишет ту же кривую, что и конец вектора W{j(a), т. е. амплитудно-фазовую характеристику разомкнутого контура автоматической системы.

Представим полином D (/со) и Q{ja) в виде

D ija) = I D (/со) I ехр [jipa ( )]- Q (/ ) = 1 Q (/ ) I ехр []% (со)], тде tj)i)((!l>) - аргумент полинома £>(/о>); x1)q((!l)) - аргумент полинома

Q (/ )

Тогда

(/ ) = Iflgl ехр / [ ((О) -я;<, ( )] = ! \V, (/со) ] е

где llJ?i(/cu)=D(/cu)/Q(/cu) - модуль вектора Wyijo));

t)i(co)=t)o(a))-я];Q(ш) -

(2.11)

аргумент вектора Wi{ia).

При изменении частоты со от -схэ до оо вектор Wi{ja) как указывалось, опишет на плоскости UOV АФХ разомкнутой системы, совершив при этом поворот на угол Aip, определяемый в соответствии с (2. И) разностью полных приращений аргументов характеристических полиномов D{j(j)) H.Q(/a)).

Найдем полное приращение аргумента Aip вектора WQu)):

Дг)1 = Дя;о -

при изменении ш от -оо до оо для различных типов автоматических систем при условии, что замкнутая автоматическая система устойчива, т. е. по критерию Михайлова, Дг)о=пп при ш 6 (-оо, оо).

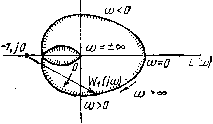Рис. 2.3

Статическая система, устойчивая в разомкнутом состоянии. Рассмотрим систему, в состав которой входят лишь устойчивые позиционные звенья, т. е. систему, все корни характеристического полинома разомкнутого контура которой имеют отрицательные вещественные части. Тогда, применяя критерий Михайлова к полиному Q(/o)), имеем Дг)д=пп и, следовательно, AtJj=At)o-Дг)д=пп-пл,=0. щ

Таким образом, вектор Wiiai), описав АФХ этой системы, не должен совершить ни одного оборота вокруг своего начала координат, т. е. вокруг точки с координатами (-1, /0) (рис. 2.3). Из рисунка ясно, что для рассматриваемой системы At)i=0 лишь в том случае, если АФХ этой системы не охватывает точку с координатами (-1, /0). Если АФХ, изображенная на рис. 2.3, охватывает эту точку, то полное приращение аргумента Дг)?! составит 8я/2.

Для дальнейшего важно отметить, что внутренняя область, ограниченная кривой Wijiii), лежит справа от этой кривой при движении по ней в направлении возрастания частоты со от О до оо и далее от -оо до 0.

Следовательно, рассматривая условия устойчивости статической автоматической системы, приходим к выводу, известному как критерий устойчивости Найквиста. Для устойчивости замкнутой автоматической системы, устойчивой в разомкнутом состоянии, необходимо и достаточ-

но, чтобы АФХ разомкнутого контура этой системы, построенная при изменении частоты ш в пределах от -оо до оо, не охватывала критическую точку с координатами (-1, /0).

Астатическая система с астатизмом первого порядка. Рассмотрим автоматическую систему, содержащую помимо устойчивых позиционных звеньев одно интегрирующее звено. Примерный вид АФХ такой системы показан на рис. 2.4. Характеристический полином разомкнутого контура

п- 1

Q(p)=pU{+t,p)

имеет один корень, равный нулю, и п-1 корней с отрицательной вещественной частью. Применяя критерий Михайлова к этому полиному, находим, что при изменении ш от -оо до оо полное приращение аргумента этого полинома Дг)д=(п-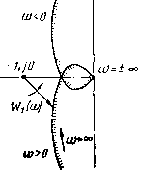

ш<0

Рис. 2.4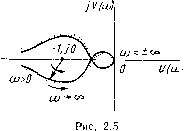

1=Д;,-=Д*я=.яя-(п-1)л=л. Это означает, что вектор 17 (/со) при изменении о от О до оо и далее от -со до О должен повернуться на угол я против часовой стрелки положительно), как показано на рис. 2.4. Из рисунка видно, что АФХ рассматриваемой системы делит плоскость на две области - внутреннюю , лежащую справа от АФХ при движении по ней в направлении возрастания частоты, и внешнюю . Как и в предыдущем случае, замкнутая автоматическая система будет устойчивой, если точка с координатами (-1, / 0) не попадает во внутреннюю область, т. е. если АФХ системы не охватывает эту точку.

Таким образом, приведенная формулировка критерия устойчивости Найквиста остается справедливой и для автоматических систем с астатизмом первого порядка.

Астатическая система с астатизмом второго порядка. Рассмотрим автоматическую систему, содержащую помимо устойчивых позиционных звеньев два интегрирующих звена. Примерный вид АФХ такой системы показан на рис. 2.5. Характеристический полино.ч разомкну-