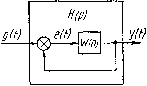Передаточная функция разомкнутой системы. Помимо передаточной функции замкнутой системы при анализе и синтезе замкнутых автоматических систем широко используют передаточную функцию разомкнутой системы. Передаточной функцией разомкнутой системы называют передаточную функцию, которая устанавливает зависимость между управляемой величиной y{t) замкнутой автоматической системы и ее ошибкой e{t), т. е., по определению,

W{p) = Y{p)lEip), (1.54)

E{p) = L[e{t)] = L[git)-y{t)]:

=С(р)-ВД.

Рис. 1.22 Для передаточной функции разомкну-

той системы примем то же обозначение W{p), что и для произвольной динамической системы (1.5).

Заметим, что в процессе определения передаточной функции замкнутой автоматической системы по ее структурной схеме мы неизбежно проходим этап определения передаточной функции разомкнутой системы. Найдем, например, передаточную функцию замкнутой системы в соответствии со структурной схемой рис. 1.16, которая представляет собой цепочку последовательно соединенных звеньев, охваченную единичной отрицательной обратной связью.

Участок структурной схемы замкнутой автоматической системы между точкой приложения ошибки e{t) и точкой фиксации выходной величины y(t) называют разомкнутым контуром автоматической системы.

В соответствии с рис. 1.16, выражением (1.48) и определением (1.54)

У (О = (Р) (Р) iP) \ov iP) eit)W ip) e\it),

W ip) = r ip) ip) ip) ip)- (1.55)

передаточная функция разомкнутой системы, соответствующая замкнутой автоматической системе рис. 1.16. Приведем схему рис. 1.16 к виду схемы, представленной на рис. 1.22. Сопоставляя схему рис. 1.22 со схемой рис. 1.19, видим, что схема рис. 1.22 может быть получена из схемы рис. 1.19, если в этой схеме положить Xi{t)=g{t), X3{t)~ =e{i), Wi(p) = W(р), 12(/7) = 1 и учесть, что главная обратная связь замкнутой автоматической системы отрицательна. Тогда на основании (1.50) находим передаточную функцию замкнутой системы:

Выражение (1.56) устанавливает связь между передаточными функциями замкнутой и разомкнутой систем, соответствующими однойи той же замкнутой автоматической системе.

из [i..DO) получим ооратную зависихмость

Н{р) Rip)

Rip)

\~Н(р) D{p)-R(p) Q(p)

(1.57)

где Q(p)=D(p)-R(p) - полином степени п.

Заметим, что выражение (1.57) может быть получено из (1.54) с учетом (1.52) и (1.53).

Роль передаточной функции разомкнутой системы в исследовании замкнутых автоматических систем чрезвычайно велика. В частности, на использовании этой передаточной функции базируется один из основных методов анализа и синтеза замкнутых автоматических систем - метод логарифмических частотных характеристик.

Передаточная функция для ошибки по задаюш,ему воздействию. При исследовании точности замкнутых автоматических систем нас интересует зависимость ошибки e(i) от задающего воздействия g{t). Эта зависимость определяется передаточной функцией для ошибки п задающему воздействию, которую обозначим Нр{р). Если передаточная функция Не{р) известна, то по ее определению имеем Е{р) =

h4p)G(p).

Чтобы найти эту передаточную функцию по заданной структурной схеме автоматической системы, целесообразно выразить ее через передаточную функцию замкнутой системы Я (/?) или через передаточную функцию разомкнутой системы W (р):

или, учитывая (1.56),

ffe(P)

1-f IF (р)-

(1.59)

После того как передаточная функция Не(р) найдена, ошибка замкнутой автоматической системы для задающего воздействия, имеющего вид конкретной функции времени g{t), может быть определена путем обратного преобразования Лапласа, т. е.

e{t) = L-[E(p)]=L-[HAp)G(p)].

Передаточная функция для ошибки по помехе. Системы радиоавтоматики работают, как правило, в условиях помех. При этом за-

ьД-<+)-

Рис. 1.23

дающее воздействие (О всегда приложено ко входу системы, а помеха a(t) может быть приложена в произвольной точке системы, как показано на рис. 1.23, где разомкнутый контур системы радио автоматики разделен на две части: первая, с передаточной функцией W-(p), не

подвержена действию помехи, а на входе второй, с передаточной функцией Wip), действует помеха v{t). При этом передаточная функция разомкнутого контура системы W{p) = W.{p)W{р)-

Выходная величина системы радиоавтоматики может быть представлена в виде Ух (0=У (0+68.(0. где У {t)=H{p)g{t) - реакция системы на задающее воздействие: е (0= i + ц(р)цУ2 (р) реакция системы на помеху.

Ясно, что составляющая еЦ) выходной величины i/i(0 искажает значение управляемой величины у (0. т. е. является ошибкой системы, обусловленной помехой v{t).

Отношение изображения Е{р) этой ошибки к изображению помехи V{p) определяет передаточную функцию системы радиоавтоматики для ошибки по помехе, т. е.

В частности, если помеха действует на входе системы, из (СбО) получаем

еЛР)-тЩ) = Н(р).

Типовые передаточные функции систем радиоавтоматики. Большинство функциональных элементов систем радиоавтоматики обладает свойствами апериодических, а также безынерционных звеньев. Помимо этих звеньев в состав систем радиоавтоматики обычно входит несколько интегрирующих и форсирующих звеньев. Таким образом, типовая передаточная функция разомкнутого контура системы радиоавтоматики может быть представлена в виде

Кг U.i + TiP)

{p) = -i- при т<п, K] = 6- (1.61)

где п-порядок дифференциального уравнения (1.7) замкнутой системы; г - количество интегрирующих звеньев в составе системы; т - количество форсирующих звеньев в составе системы; Кг- коэффициент передачи системы по г-й производной входного воздействия. Для типовых систем радиоавтоматики, рассмотренных в § 1.2, обычно т=1, /<2.

Как показано в гл. 2, качество автоматической системы (ее точность!) в сильной степени зависит от количества интегрирующих звеньев в составе этой системы. С увеличением количества интегрирующих звеньев точность существенно возрастает.

Замкнутую автоматическую систему, не содержащую интегрирующих звеньев (г=0), называют статической системой. Она имеет пере-