вместо прежнего значения x-WiX. Соответственно изменится и выходная величина Ха- Чтобы величину сохранить неизменной, необходимо xi умножить на передаточную функцию W~l{p), обратную передаточной функции (р), что означает необходимость включения последовательно со звеном Wj звена W~l, как показано на рис. 1.20, в. Действитатьно, для схемы рис. 1.20 в имеем

x, = W, (х, + X,) = Г 3 (Гл + W.Wrx,} = = W, (Г л + W,W:W,x,) = W, (W, + W,) х

что совпадает с (1.51).у

Пусть теперь в схеМе рис. 1.20, а необходимо перенести сумматор со входа звена W3 на его выход. Поскольку в выражении (1.51)

Эпемент сравнения

Сумматор sj...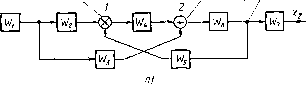

Збена

wj- к/у

П г

I L.

Рис. 1.21

является общим множителем для величин х и х, являющихся выходными величинами звеньев и W, то для сохранения неизменного значения х следует звено с передаточной функцией з{р) включить последовательно с каждым из звеньев и W, как показано на схеме рис. 1.20, г, для которой

х,х,Л-х, = W,W,x + ГзГл = Г 3 (Г, + Г,) ж

что тождественно выражению (1.51).

Наконец, перенесем в схеме рис. 1.20, а сумматор с выхода звена Wi на его вход. Получим схему рис. 1.20, д, для которой

x, = W3W, (x, + лгз) = W3W, {W,x, + x,) = Гз {W,W, + Г,) x,

Таблица 1.1. Правила преоЗразования структурных схем линейных систем

Операция

Исходная схема

Эквивалентная схема

Перестановка суммато ров или элементов срав нения

Перестановка звеньев

Перенос узла с выхода навход сумматора

0--ЕР*

Перенос узла с входа на выход сумматора

Перенос узла с выхода на вход звена

Перенос узла с входа на выход звена

Перенос сумматора с выхода на вход звена

Перенос сумматора с входа на выход звена

Замена звеньев прямой и обратной цепей

Переход к единичной обратной связи

вместо (1.51). Ясно, что х, останется неизменным при данном структурном преобразовании лишь в случае, если последовательно со звеном Wi включить звено как показано на схеме рис. 1.20, е, для которой находим

X, = Г зГ, (х, + X,) = ГзГ, (Г Гл + = Гз (Г, + Г,) х

что совпадает с (1.51).

Читателю рекомендуется найти отношение выход - вход для всех схем табл. 1.1 и убедиться, что для каждой пары эквивалентных схем эти отшшения тождественны.

Пример 1.5. Рассмотрим структурную схему рис. 1.21, а. В этой схеме перекрестные связи обусловлены наличием между сумматорами 7 и 2 звена if4. Чтобы избавиться в этой схеме от перекрестных связей, достаточно, например, сумматор 1 перенести со входа звена W на его выход. При этом получим схему рис. 1.21,6 и, поменяв сумматоры местами, придем к схеме рис. 1.21, в, для которой в соответствии с формулами (1.48) - (1.50) имеем

откуда

=xrS= =

IFi (р) {(р) W, (р) + if3 (Р)] (р) W, (р) l+lF,(p)W7,(p)lFe(p)

Передаточная функция замкнутой системы. При исследовании автоматических систем возникают различные задачи, например определение характеристик переходного процесса в системе, определение ее точности, помехоустойчивости и т. д. Решение этих задач требует установления зависимостей между различными переменными автоматической системы, например, между выходной и входной величинами системы, между ошибкой и входной величиной и т. д. Эти зависимости устанавливаются посредством соответствующих передаточных функций автоматической системы.

Так, процесс управления характеризуется зависимостью управляемой величины y{t) от задающего воздействия g(t). Эта зависимость определяется передаточной функцией замкнутой системы (1.9), которая может быть найдена методами, изложенными в § 1.3, если заданы структурная схема системы и передаточные функции ее звеньев.

Чтобы получить выражение передаточной функции замкнутой системы в общем виде, будем исходить из дифференциального уравнения этой системы (1.7).,Тогда в соответствии с (1.8) и (1.9), переходя к изображениям Лапласа, имеем

Y{p)H{p)G{p), (1.52)

\H(p)=Y{p)lG{p) = R{p)lD{p). (1.53)

Здесь R (р) - полином степени т; D(p) - полином степени п.

Передаточная функция замкнутой системы является одной из основных передаточных функций замкнутой автоматической системы.