торой указывают динамические звенья системы и связи между ними. Такую схему называют структурной схемой автоматической системы.

Структурную схему получают из функциональной, замещая обозначения функциональных элементов системы обозначениями или явными выражениями передаточных функций этих элементов. Так, на рис. 1.16 представлена структурная схема, составленная на основании функциональной схемы рис. 1.2.

Рис. L.16

Структурная схема автоматической системы позволяет получить передаточную функцию или дифференциальное уравнение этой системы при известных динамических характеристиках ее звеньев, как это было показано на примере простейшей в структурном отношении системы (§ 1.3).

При определении передаточной функции достаточно сложной автоматической системы ее структурную схему упрощают, пользуясь методами преобразования структурных схем, позволяющими перейти от сложных перекрестных соединений звеньев в системе к некоторым простейшим, типовым соединениям. Существует три вида таких соединений: последовательное, параллельное и встречно-параллельное, или охват обратной связью одного звена посредством другого.

Рис. 1.17

Последовательное соединение звеньев. Последовательным называют такое соединение звеньев, при котором, как показано на рис. 1.17, выходная величина одного звена является входной величиной другого. В соответствии с рис. 1.17 имеем

K.r{t) = W (р) xi (/) = Г (р) х (О = Г {р) W , ip) х , (t) =

= ... = wap) w ,{p)- хЛр)хЛр)х.(0.

откуда

W (р) = W, ip) г, {р)... Г , (р) Г (р). (1.48)

Таким образом, при последовательном соединении звеньев передаточная функция такого соединения равна произведению передаточных функций отдельных звеньев.

Выражение (1.48) справедливо при условии, что соединение выхода каждого k-To звена со входом следующего, (fe+l)-ro звена не изменяет

передаточную функцию k-ro звена. В противном случае передаточную функцию Whip) к-то звена нужно составлять с учетом влияния следующего звена.

Параллельное соединение звеньев. При параллельном соединении звеньев, как показано на рис. 1.18, входная величина Jti() поступает на входы всех звеньев, входящих в это соединение, а выходная величина xit) равна сумме выходных величин отдельных звеньев, т. е.

x,{t)W{p)x,{t)==J, W,ip)xAt)

k - 1

2 w,ip)

X, it),

откуда

(1.49)

Таким образом, передаточная функция сложного звена, состоящего из п параллельно соединенных звеньев, равна сумме передаточных функций отдельных звеньев.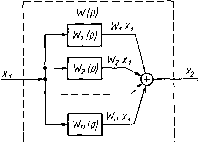

Wfp}

Рис. 1.18

Рис. 1.19

Охват звена обратной связью (встречно-параллельное соединение двух звеньев). Схема звена, охваченного обратной связью, показана на рис. 1.19. Как видно из схемы, на вход звена с передаточной функцией Wi{p), охваченного обратной связью посредством звена с передаточной функцией Wi{p), поступает сумма или разность (в зависимости от характера обратной связи) двух величин - входной Xi(0 и выходной xit), прошедшей через звено обратной связи.

В обозначениях рис. 1.19 имеем

X, it) =x,it)±x,{t), X, (t) = ip) x,{t),

откуда

2 (0 = ip) X, (0 = г iP) X, (t) = ip) [X, (t) ± W, ip) X, it)].

Окончательно получаем

W{p)==

1 T Wi (p) W, (p)

(1.50)

где знак минус соответствует положительной обратной связи, а знак плюс - отрицательной.

Преобразования структурных схем линейных систем. Рассматривая структурные схемы линейных автоматических систем, видим, что любая структурная схема состоит из элементов трех типов: звеньев, узлов и сумматоров, соединенных между собой связями, как показано, например, на рис. 1.20 и 1.21. Элемент сравнения, имеющийся в составе структурной схемы рис. 1.21, является частным случаем сумматора, на выходе которого образуется разность двух его входных величин.

узел

Здено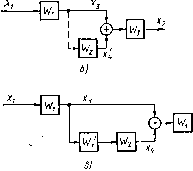

w, -,

Рис. 1.20

Если В структурной схеме исследуемой системы имеется участок, содержащий сложные перекрестные связи, не сводящиеся к рассмотренным простейшим соединениям звеньев, то этот участок выделяют и подвергают структурным преобразованиям с целью приведения всех его соединений к простейшим типовым. Структурные преобразования состоят в изменении взаимного расположения элементов структурной схемы (звеньев, узлов и сумматоров) таким образом, чтобы, не изменяя входных и выходных величин преобразуемого участка схемы, изменить (упростить) характер соединений его звеньев.

Правила изменений взаимного расположения элементов структурной схемы определяются табл. 1.1. Поясним смысл этих правил на примерах. Пусть имеется исходная структурная схема динамической системы рис. 1.20, а. Для этойсхемы имеем

X, = Г 3 (хз + X,) = Wli Г л -\- W,x,) = Г 3 (Г, -Ыз) X,. (1.51)

Допустим, что требуется перенести узел со входа звена W- на его выход. После такого переноса (рис. 1.20, 6) значение х на входе сумматора не изменилось, а значение x стало равным Xi=W2X-i=W-х.