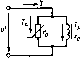Рис, 6.30. Схема замещения идеализированной обмотки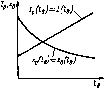

Рис. 6.31. Зависимость Zq{V)v =кхо{С/) идеализированной обмотки

Рис. 6.32. Зависимость /,(/5) и ха{1ь) Шъ) идеализированной обмотки

Zq[V) Xo{V). Такой график для одного из воздушных зазоров приведен на рис. 6.31.

Как видно, в отличие от электромагнитных устройств с постоянной МДС, у которых сопротивление обмотки не зависит от напряжения на ее выводах, у электромагнитных устройств с переменной МДС полное сопротивление обмотки (равное примерно ее индуктивному сопротивлению) с увеличением напряжения изменяется. Пока напряжение относительно невелико и материал магнитопровода не насыщен, сопротивление обмотки остается примерно постоянным; по мере увеличения напряжения и степени насыщения ферромагнитного материала сопротивление значительно уменьшается.

Представляет интерес характер изменения тока и сопротивления идеализированной обмотки при увеличении воздушного зазора в магнитопроводе.

Пренебрегая активной составляющей тока ввиду его малости, можно написать

/p.c + B 4/l/2wpo. (6.38)

1К1 = / с + h

Сопротивление катушки будет Zo Хо = U/Ip =

(6.39)

С увеличением воздушного зазора при u = const все члены в правых частях выражений (6.38) и (6.39), кроме длины воздуш-

ного зазсфа 4, остаются постоянными. Графики зависимостей /р(4) к /(4) и X(j(4) * построенные в соответствии с вы-

ражениями (6.38) и (6.39), приведены на рис. 6.32.

В отличие от электромагнитных устройств с постоянной МДС, укоторых с увеличением воздушного зазора при 11 = = const сопротивление и ток обмотки остаются постоянньпии, у электромагнитных устройств с переменной МДС уиеличение воздушного зазора приводит к значительному уменьшению сопротивления и увеличению тока.

Последнее во многих случаях является весьма нежелательным, так как приводит к увеличению габаритных размеров обмотки, потребляемой индуктивной мощности и к ухудшению энергетических показателей электромагнитных устройств. Поэтому, например, в трансформаторах, магнитных усштителях и двигателях переменного тока стремятся воздушные зазоры свести к минимуму. У электромагнитов различных электротехнических аппаратов, у которых воздушный зазор необходим, исходя из принципа их действия (тормозные электромагниты, контакторы, реле и др.), приходится специально рассчитывать обмотку по нагреванию с учетом повышенных значений начальных токов, возникающих в момент подключения обмоткн к источнику, когда подвижная часть магнитопровода - якорь - еце не притянулась к неподвижной части магнитопровода и воздушный зазор не ликвидирован. Для таких устройств в справочной литературе указывается обычно наибольшее допустимое число включений в час, на которое рассчитана обмотка, исходя из ее дополнительного нагревания начальными токами.

Однако зависимость тока и сопротивления обмотки переменного тока от воздушного зазора не всегда оказывается нежелательной. Указанная зависимость широко используется в устройствах автоматики и измерительной техники, примером чему могут служить индуктивные конечные и путевые выключатели, индуктивные датчики для измерения неэлектрических величин.

В § 6.13 было сказано, что показатель степени п в (6.32) дяя многих ферромагнитных материалов близок к двум. В этом случае при/= const ДР = fct/ и согласно (6.37) получим

- Г772-

ДР, kV

Таким образом, сопротивление Tq схемы замещения почти постоянно и зависимость u{I) близка к линейной.

6.1S. СХЕМЫ ЗАМЕЩЕНИЯ. ВЕКТОРНЫЕ ДИАГРАММЫ

И МОЩНОСТИ РЕАЛЬНОЙ ОБМОТКИ

С ФЕРРОМАГНИТНЫМ МАГНИТОПРОВОДОМ

После замены нссннусоидального тока идеализированной обмотки эквивалентным синусоидальным током для реальной обмотки (см. рис. 6.21,я) на основании второго закона Кирхгофа можно написать следующее уравнение:

(6.40)

Возникшая от магнитного поля рассеяния ЭДС Ер учитывается обычно как падение напряжения в индуктивном сопротивлении:

где Lj и Х =ci)L, - индуктивность и индуктивное сопротивление, обусловленные полем рассеяния.

Так как линии магнитной индукции поля рассеяния проходят преимущественно по воздуху, можно считать = const и Xj = const.

После замены в (6.40) комплекса ЭДС £р его выражением получим

f/=f/ + /r,-ьДх,. (6.41)

Дополнив в соответствии с уравнением (6.41) диаграмму, изображенную на рис. 6.28, векторами падений напряжения, получим диаграмму реальной обмотки с ферромагнитным магнитоироводом (рис. 6.33).

В соответствии с (6.41) и векторной диаграммой (рис. 6.33) можно получить схему замещения реальной обмотки, дополнив схему замещения идеальной обмотки резистивными и индуктивным x элементами, соединенными последовательно. Схема замйцения реальной обмотки дана на рис, 6.34.

Как следуетиз уравнения (6.41) и векторной диаграммы рис. 6.33, вследствие падений напряжения /г, и /х, напряжение U = Е оказывается меньше напряжения U, подводимого к обмотке. С изменением тока /, вызванным, например, изменением воздушного зазора, напряжение U\ ЭДС Е и магнитный поток Ф будут изменяться. При этом ток / будет изменяться в меньшей степени, чем в случае ндеализироваиной катушки. Следует, однако, нметь в виду, что при нормальных условиях работы многих электромагнитных устройств напряжение U = Е значительно, превышает падения напряжения /г и /х, и близко к на-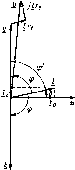

Рис. 6.33. Векторная диаграмма реальной обмотки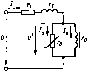

Рис. 6.34. Схема замещения реальной обмотки

пряжению и. В соответствии с этим полное сопротивление схемы замещения идеализированной обмотки Zo Хр (см. рнс. 6.31) значительно превышает сопротивление Zi = ]/rf-i- xJ и близко к эквивалентному полному сопротивлению z реальной катушки.

Активная и реактивная мощности реальной обмотки отличаются от соответствующих мощностей идеализированной обмотки и могут быть выражены следующим образом. Активная мощность

?={ со5ф. (6.42)

Из векторной диаграммы рис. 6.33 следует, что Ucos(p =

= Ir, + {/СОЗф.

Учитывая ЭТО, активную мощность можно выразить так: P = lh, + Ul cos ф = 11 + Vh = Аобм + (6.43)

Как видно, активная мощность Р, потребляемая реальной обмоткой, равна сумме потерь мощности в обмотке (ДРбм) и потерь мощности в ферромагнитном магнитопроводе (APJ.

Аналогичные выражения можно написать и для реактивной мощности:

Q = Ulsia ф = Pxi + Ul sin ф = Рх + С Тр = Qp + Q. (6.44)

Мошность Qp необходима для возбуждения магнитного по-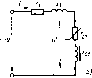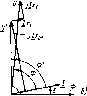

Рис. 6.35. Схема замещения и векторная диаграмма реальной обмотки с последовательным соединением резистивных и индуктивных элементов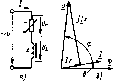

Рис. 6.36. Простейшая.схема замещения и векторная диаграмма реальной обмотки

ля рассеяния, мощность Q - д.тя возбуждения основного магнитного поля.

Как известно, параллельно соединенные элементы электрической цепн могут быть заменены эквивалентными элементами, соединенными последовательно. Учитывая это, в схеме замещения рис. 6.34 элементы и можно заменить последовательно соединенными элементами г, н и получить более простую схему замещения реальной обмотки, изображенную на рис. 6.35, а. Так как г, то после указанной замены получим (см. гл. 2). После объединения резистивных, а также индуктивных элементов в схеме рнс. 6.35, а получим еще более простую схему замещения реальной обмоткн (рис. 6.36, а). Естественно, что в последней схеме сопротивление X = + Х намного больше сопротивления г = Гщ + г. Векторные диаграммы, соответствующие схемам замещения рис. 6.35,а н 6.36,й даны иа рнс. 6.35,6 и 6.36,.

6Л6. ОПРЕДЕЛЕНИЕ ТОКА, МОЩНОСТЕЙ, ЭКВИВАЛЕНТНЫХ СОПРОТИВЛЕНИЙ И УГЛА СДВИГА ФАЗ МЕЖДУ НАПРЯЖЕНИЕМ И ТОКОМ РЕАЛЬНОЙ ОБМОТКИ

Поскольку схема замещения реальной обмотки с ферромагнитным магинтопроводом (см. рнс. 6.34) представляет собой смешанное соединение различных по характеру линейных и нелинейных элементов, определение тока, мощностей, эквивалентных сопротивлений и угла сдвига фаз тока относительно напряжения источника реальной обмотки значительно осложняется.

Предположим, что при заданном синусоидальном напряжении и источника требуется получить в магнитопроводе с известными геометрическими размерами магнитный поток Ф.

Определение указанных выше величин может быть произведено методом последовательного приближения в следующем порядке.

Так как в сопротивлениях н х, (см. рис. 6.34) теряется часть напряжения, то принимают напряжение V несколько меньшим нттряжеиия U источника. Пусть, например, U = = и [ = 0,91/. Задавшись напряжением U J, из формулы (6.27) нетрудно определить прн потоке число витков w катушкн.

Далее, в соответствии с методикой, изложсшюй в § 6.13, следует найти токн /а, 1р и /.

Зиая ток /, нужно задаться (исходя из нагревания) плотностью тока / и подсчитать площадь поперечного сечения проволоки катушки. Задавшись коэффициентом заполнения (см. § 6.8), необходимо изобразить эскиз катушки, определить длину среднего витка, а затем сопротивление катупгки.

Сведения об определении индуктивного сопротивления рассеяния Xi можно найти в литературе по расчету соответствующих электромагнитных устройств. Рели степень насьпцения ферромагнитного материала прн максимальном значении магнитной индукции и воздушные зазоры в магнитопроводе невелики, то для ориентировочного определения сопротивления Xj можно воспользоваться формулой

х,=(1,5-2,5)г,.

Для дальнейшего расчета целесообразно использовать комплексный метод. Совместив, например, мысленно ось мнимых величин с вектором напряжения t/, следует выразить напряжение t/j, а также токи 1, /р и / в комплексной форме.