Полставив значения р, н А, в (4.51). получим

IjaL L

(4.55)

На рис. 4,9,(1 (пображсн график Ток изменяется но )акону. нрсдставляющему собий произведение сииуспнлы с ампчитудой V/inL на пока1ательную функцию. В идеа.льиом случае, когда г = 0, возникнут синусоидальные колебания с нсюмснноЗ амплитудой,

Дсйстзительно, при г = 0. Р = 0, ш = ток

-sin Од/,

4 S6I

а частота и период нсзатухающил колебаний

а.(, = !Д.-. Т= ! = 2тг/а)о

На рнс. 4.9,в пунктирной линией изображен график незатухающих ко.пебаний.

4.10. ЭЛЕКТРИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ МЕХАНИЧЕСКИХ И ДРУГИХ СИСТЕМ

Разработка новых сложных механических, гидравлических и других систем связана со значительными трудностями, состоящими в том, что Hci гарантии получения требуемых расчетных величин и лет возможности провести зксоеримен-тальные исследования системы, поскольку она не выполнена в натуре. Поэтому при разработке той или иной системы прибегаю! к созданию физической модели системы. Результаты исследования модели позволяют выяни1ь действительные характеристики и дать рекомендации для корректировки параметров системы с целью получения оптимальных характеристик. Наиболее простыми и универсальными моделями для иси1едо-вання как стационарных, так и переходных режимов механических и других систем являются электрические модели, представляющие собой злектрические цепи с резистивными, емкостными II индуктивпьпии элементами, в которых аналогами исследуемых ве.тчин являются ток, напряжение, индуктивность и емкость. Выполнение хтсктрической модели и проведение ее исслсдовапня vx свячано с какими-либо техническими трудностями и не требует знач1ттсльных затрат. Создание же механи-172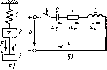

Рис. 4.10. Механическая система {а\ и ее sjrcR [рическан модель (6)

ческой модели связано со значительными трудностями и капитальными затратами.

Электрическая модель будет соответствовать реальной системе, если математическое описание мидели и системы одинаковое.

Рассмотрим электрическую модель механической системы, изображенной на рис. 4.10, а. Механическая система состоит нз тела 2 с массой т, пружины 1 и воздуш. ного демпфера 5, состояп1его из поршня, расположенною в цилиндре. Допустим, тело 2 удерживалось в неподвижном состоянии внешней силой, когда пружина / была ненапряженной. После удаления внешней силы под действием силы тяжести система придет в движение. Тело начнет опускаться, пружина -растягиваться, появится демпфирующая сила демпфера. Возникнет переходный процесс, который постепенно затухнет и система снова окажется в неподвижном сосгоянии. Электрической моделью рассмотренной механической системы является электрическая цепь с резистивным, индуктивным и емкостным элементами, изображенная на рис, 4.10, 6. так как дифференциальное уравнение переходного процесса этой цепи при подключении ее к источнику с постоянным напряжением аналогично дифференциальному уравнению переходного процесса механической системы.

Уравнение движения механической системы имеет внд

F~Fi-F2=m dv/dt,

где f - сила тяжести массы; f, = к,х- упругая сила пружины; f J =i,(! - сила, развиваемая демпфером; х - перемещение тела от начального положения; г - скорость тела. Таким образом, для механической системы

F = kjX + k2V +т dv/dt. (4.57)

Уравнение переходного процесса электрической цепи

и =uc-i-u,+ Ui, -i-j J dt + ir -\- L di/dt. (4.58)

Из сравнения уравнений (4.57) и (4.58) следует, что напряжение и, приложенное к цепи, является аналогом силы F, приложенной к механической системе, напряжение с на емкости -

аналогом силы, развиваемой пружиной, ток i цени - аналогом скорости и, - аналогом силы, возникаюшей в демпфере, индуктивность L- аналогом массы lejia m.

Таким образом, благодаря единпну уравнений электрической цепи и механической системы исследшиние явлений в механической системе может быть произведено с помощью исследования переходных процессов электрической цепи. Характер переходного процесса механической системы, так же как и ее электрической модели, может быть апериодическим или колебательным. В механической системе он определяется соотношением массы тепа, упругости пружины и демпфирующей силы демпфера, в электрической модели, как это доказано в § 4.9, - соотношением параметров цепи г, L, С.

Резу.1гьтаты решения уравнения электрической цепн будут отображать характер и дли1ельнасть переходного процесса механической системы, если соблюдены соответствующие соотношения между параметрами механической системы и ее моделью - электрической цепью. Соотношения устанавливаются посредством масштабньи коэффициентов. Значения и размерность масштабных коэффициентов можно установить, если разделить почленно уравнение (4.58) на уравнение (4.57).

В результате получим

~= К] B/Hi [и,] В/Н;

1- - [ iM !,] Ом мДН с) А с/м = В/Н;

= [ т ,л] Гн . м/(Н с). А. с V(c м) = В/Н.

Выразив в уравнении (4.57) соответствующие величины через масштабные коэффициенты, получим уравнение электрической цени с учетом масштабных коэффициентов и иг п Ldi/dt

trip

Глава пятая

ПЕРИОДИЧЕСКИЕ НЕСИНУСОИДАЛЬНЫЕ ЭДС, ТОКИ и НАПРЯЖЕНИЯ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ

5.1. ПРИЧИНЫ ВОЗНИКНОВЕНИЯ ПЕРИОДИЧЕСКИХ НЕСИНУСОИДАЛЬНЫХ ТОКОВ И НАПРЯЖЕНИЙ

В предыдущих главах был рассмотрен расчет и анализ электрических цепей синусоидального тока. Однако на практике при генерировании, трш1сформацнн, распределении и потреблении электроэнергии возЕшкают искажения формы синусон-дальпых ЭДС, напряжении и токов.

Рассмотрим основные причины возникновения периодических несннусоидальиых токов и напряжений.

Несинусоидальиые токи в цепях возникают нри синусоидальных ЭДС и напряжениях источников электрической энергии, если цепи содержат нелинейные элементы. Так, в катушке с рроматнитным магинтопроводом, которая является нелинейным элементом прн синусоидальном напряжении сетн ток несинусондалъный. Подобное явление наблюдается в промышленных городских сетях, когда в качестве осветительных приборов используются люминесцентнью лампы, имеющие нелинейные вольт-амперные характеристики. На рнс. 5.1 показана схема включения люминесцентной ламт : Л в сеть синусоидального напряжения с ограничивающим дросселем L, работающим в линейном режиме, а также приведены графики юка и напряжения на лампе.

Нелинейные элементы широко используются в электрических цепях автоматики, управления, релейной защиты и т. д. Эги нелинейные элементы (стабилизаторы напряжения, у\шо-житепи и делители частоты, магнитные уси.чнтели и т. п.) приводят к искажению формы кривых напряжения или тока.

Известно, что постоянный ток в энергетической электронике получают преобразованием переменного синусоидально] о юка с помощью выпрямителей, в которых использую! си нелинейные элементы - диоды (полупроводниковые, электронные и ионные). Естественно, что в таких электрических цепях возникают как несииусоидальные токи, las и несинусоидальные напряжения, На рис. 5.2 приведены временные диаграммы напряжений и токов однополупериодного, двухполупериодного и 1рехфа?ного выпрямителей, работающих на резнстнвпую нагрузку.

Рис. 5.1. CxeMti включения и временные диаграммы тока и напряжения люминесцентной лампы

Рис. 5.2. Временные диаграммы напряжений и токов в нагрузке однополупсриодного (а), двухпо-лупсриодного (б) и Tpexil>ajHuio (в> выпрямителей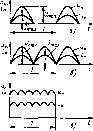

В настоящее время широкое распространение получила импульсная техника, т, е. отрасль радиоэлектроники, в которой для решения определенных задач использую i импульсные устройства. Режим работы подобных устройств характеризуется чередованием времени работы и пауз. Формы импульсов напряжений в импульсной технике весьма разнообразны. Основное распространение получили импульсы треугольной, прямоугольной, трапецеидальной формы и др. (рис. 5,3. а - в). В связи с этим появилось значительное разнообразие схем импульсных генераторов несинусондальных колебаний. Такие генераторы называю1ся релаксационными, т, е. нх форма колебания выходных сигналов в значительной степени огличается от синусоиды

Например, к рслаксапионным тенераторам относится генератор пилообразного напряжения. Пилообразные импульсы напряжения (рнс. 5.4) используются в устройствах сравнения, для горизонтальной развертки электронного луча в электронно-лучевой трубке, в радиолокационной и радиоизмернтельной технике я т. д. Для формирования прямоугольных импульсов напряжения, широко применяемых в различных схемах импульсной и вычислительной текинки, использую1ся релаксационные генераторы - мультивибраторы.

Появление в электрических цепях несннусоцдальных напряжений и токов может привести к весьма нежелательным последствиям. Несинусоидальные токи вызывают дополнительные потери мощности, ухудшают характеристики двигателей, создают болыпие помехи в линиях связи, каналах телемеханики и т. д. Заметим, что допустимое содержание i ар-

Рис. 5.3. Формы импульсов напряжений, используемых в импульсной технике: а - треугол1.110го; 6 - прямоугольного; в - трапецеидального

Рис, 5.4. Временная диаграмма пилообразного напряжения

МОНИК оценивается коэффициентом гармоник (см. с. 181). Так, согласно ГОСТ 13109-67 (нормы качества электрической энергии) для промышленных сетей fcp 5%, т, е. в этом случае кривая напряжения на экране осциллографа визуально не отличается от синусоиды и это напряжение длительно допустимо на выводах любого приемника электрической энергии

5.2. СПОСОБЫ ПРЕДСТАВЛЕНИЯ ПЕРИОДИЧЕСКИХ НЕСИНУСОИДАЛЬНЫХ ВЕЛИЧИН

Периодические песинусоидальные величины могут быть представлены временными диаграммами, тригонометрическим рядом Фурье, а также эквивалентными синусоидами. Наиболее наглядными, дающими полное представление о несинусоидаль-ной величине являются временные диаграммы, т, е. графики за-ВИСИ.МОСТН мгновенных значений от времени (рис. 5.2-5,4).

Несинусоидальные ЭДС, токи и напряжения, с которыми приходится встречаться в электротехнике и промышленной электронике, являются периодическими функциями, удовлетворяющими условиям Дирихле и, следователыю, могут быть представлены тригонометрическим рядом Фурье:

/(coc)-4o + -imSin(cur-b<l/,) + /i2 sHi(2(Dn I ... У

А %\п(кШ -I-

где /1) - носгоянная составляющая; sin (ш(-1-i) - основная или первая гармоника, частота которой со = 2тг/Т равна