шунтирующего резистор г,. Параметры цепи: г = 1000 Ом, г, = = 4000 Ом, t; = 200 В.

Решение- До замыкания выктючатсля ток в цепи

- = П,П4 А.

После замикання значение при ! = U тогда

1000 + 4000 штеля ток должен сохранить прежнее / - /ii, - 0,04 А.

Из уравнения, составленного по второму закону Кирчифа, определяем начальное значение ЭДС е:

при г =0

е - Ьн = hr -и 0,04-1000 - 200 = - 160 1

4.7. ПОДКЛЮЧЕНИЕ ЦЕПИ С ПОСЛЕДОВАТЕЛЬНО СОЕДИНЕННЫМИ РЕЗИСТИВНЫМ г И ЕМКОСТНЫМ С ЭЛЕМЕНТАМИ К СЕТИ С ПОСТОЯННЫМ НАПРЯЖЕНИЕМ

Допустим, что до включения цепи конденсатор был не заряжен. После замыкания выключателя (рис, 4.7, а) конденсатор начнет заряжаться в результате н пронодах возникнет ток и между обкладками конденсатора появится напряжение Нс-

Уравнение цепи, составленное по второму закону Кирхгофа, имеет вид

О = (Г + с - V.

(4,40)

Так как ток в цепи

а заряд q = Cuc, то

i - С duc/di. Подставив выражение тока г в (4.40), получим Сг ducfdt + Uc=U.

(4,41)

Рис. 4,7 Зависимости /(/), udt) (Й) при подключении иепи г, С (а) к сети с постоянным напряже[шем

а) . О 5) t

В эюм случае, так же как и при анализе переходных пропес-соа в цепях с индуктивностью, напряжение на емкости в переходный период состоит из двух слагаемых:

ис = с, + с.., (4-42)

где UcvcT - напряжение на емкости после окончания переходного процесса; Uc - свободная составляющая напряжения, которая после окончания переходного процесса обращается в нуль, Дифферснгщальнос уравнение (4.41) без правой части Сг ducJdt + Uf:o = 0

имеет решение

(4-43)

Показатель степени р является корнем характеристического уравнения Сгр+ 1-0:

где Т= гС - постоянная времени цепи, состоящей из последовательно включенных г и С.

Подставив в (4.43) р--УТ, получим

Напряжение на емкости

После окончания переходного процесса (заряда конденсатора) ток в цепи прекратится и, как вытекает из выражения (4.40), напряжение на емкости окажется равным напряжению сети:

су=г = и.

Значение А опреле.1ЯЮТ с помошью второго закона коммутации: при ( - w = 0.

Таким образом, напряжеиие на с-кости в переходный п .чшод

Uc = V - Ue-i с. (4,44)

Подставив Uc в (4.40), получим выражение для тоа V

I = - е-Т j4 45)

На рис. 4,7,6 изображены рифики напряжения на емкости Uc и тока 1 при включении цепи рис. 4.7, д.

Пример 4.4. Определить постоянную времени и длительность переходного процесса при включении цепи, изображенной на рис. 4.7, л. Параметры цепи: г= 10000 Ом, С = 80 мкФ. Решение. Постоянная времени цепи

Т=гС- 10000-80-10-* = 0,8 с. Длительность переходного процесса

1 = 47=4.0,8-3,2 с.

4.8. РАЗРЯД КОНДЕНСАТОРА С НА РЕЗИСТИВНЫЙ ЭЛЕМЕНТ г

После размыкания выключателя (рис 4-8, я) напряжение uc вызовет в цепи ток / и конденсатор начнет разряжаться. Энергия электрического поля за время разряда преобразуется в теплоту в сопротивлении г. Уравнение цепи, составленное по второму закону Кирхгофа, имеет вид

(4.46)

Выразив получим

О = Hf - н. (4.46) ток через емкость и напряжени<

так как i= - С duc/dt (рис. 4.8, а).

Решением дифференциального уравнения бучет ныражение Uc = Ае

Значение р определяют i

характеристического ypai

Сер 4

где Т= гС - постоянная времени цепи. 168

Рис. 4.8. Зависимости (((), ис<() (б) при отключении цепи г. С (я) от сети с постоянным напряжением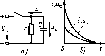

Значение А определяют с помощью второго закона коммутапии: при ( = 0+ i/f = 1- и

Таким образом,-натфяжепие на емкости при разряде конденсатора

ис = t/fi- .

(4.47)

Уравнение для . (4.46):

цени получают после подстановки мс i = -e-\ (4.48)

На рис, 4,8,6 изображены графики тока в цепи и напряж емкое!и при разряде конденсатора.

4.9. РАЗРЯД КОНДЕНСАТОРА НА КАТУШКУ С г. I

Допустим, 410 конденсагор С (рис, 4.9,й) был включен а сеть постоянного тока и, следовательно, заряжен до напряжения сети [..

После переключения выключателя из положения а в положение б конденсатор окажется замкнутым на цепочку г, L. Под действием па-пряжения На конлснсаюре с в непи возникнет ток и конденсатор начнет разряжаться Уравнение цепи, составленное по второму закону Кирхгофа, имеет вид

е = \г с. (4.49)

Выразив в (4 49) е через ток и индуктивность е = -L di/dt.

а Uc - через ток и емкость

i л 1 ,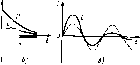

Рис. 4.У. Зависимости ilj) при апериодическом (б) и колебательном (в) разрядах конденсатора на сопротивление г и индуктивность L цепи (й)

Взяв производнуто от левой и правой частей уравнения, получим дифференциальное уравнение второго порядка без правой части

f di i

Решением дифференциального уравнени

1 = Aie- + A2e> .

(4,50)

ыражение

(451)

Корнями характеристического уравнения + у J* + = будут

Обозначив r/2L = Э и 1/iC = <oJ, получим

Р,.2= -Р±/Р- ;- -Р±Г,

Значения н определяют из начальных условий с помощью первого и второго законов коммутации

По первому закону коммутации прн f = 0 i=0 и из (4.51) вытекает.

По второму закону коммутации нри f=0 а,

(4.52)

Таким образом, в первый момент после замыкания цепи, как азс-дуег из (449), ЭДС равна - V. так как - = 0.

е = ~L di/JI--и.

Производная тока по времени из выражения (4.5!) будет равна dijdt = /liPicP + Ае = VfL.

При ( = 0

AiPi +A2P2-V/L. Из совместного решения (4.52) и (4.53) получим

(4.53)

Ai=-

т- -Аг

Выразим Pt и через р и у: V

2Ly-

Следовательно, выражение дтя тока в переходный период будет иметь вид

2Ly 2Ly

(454)

Характер переходною процесса зависит от соотношения параметров г, L, С цепи и определяется корнями характеристического уравнения.

При ]/CL<{r/2L] корни будут действительными;

-Р+Т, Р2 =

и переходный процесс будет иметь апериодический характер;

i = Л- i- *ru jl-e - w +y) = r + i . 2Ly 2Ly

Графики тока для ттого случая изображены на рис. 4.9,6. При (r/2L] < IfLC корни характеристического уравнения оказываются комплексными сопряженными:

р, - + Рз--Р-/ ,

где р - с/21; со = УМЕС (г/2-.

Значения и 2 в этом случае будут равны