4.4. ПОДКЛЮЧЕНИЕ КАТУШКИ С г, L К СЕТИ С СИНУСОИДАЛЬНЫМ НАПРЯЖЕНИЕМ

Уравнение для цепи рнс. 4.4, а, составленное по второму закону Кирхгофа, имеет вид

e = ir- и. (4.26)

Выразив в (4.26) напряжение и через амплитудное значение и ЭДС е - через индуктивность и скорость изменения тока, получим дифференциальное уравнение

L di/dt + ir = С sm(Mf + \/).

Решение дифференциального уравнения для свободною тока

L dijdt + ir - О

имеет вид

Ае .

Показатель степени р определяют из характеристического уравнения Lp + r-Q: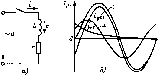

Рис, 4 4. Зависимости i{t), /уст(0. св(). () при подключении иепи г, L (а) к сети с синусоидальным иа[1рнжением

А---sm(*; - ф).

После подстановки А в (4.27) получим

£ =-sin(Mf + ф - ф)--sin(il/- ф)е Т (4.28)

где Т= L/r - постоянная времени цепи. Ток в цепи в переходный период

(4.27)

Ирнцужденный ток в цепи после окончания переходного Процесса определяют по закону Ома:

уст Sin(Mf -(- ф - ф).

z = Yr+x\ ф =

arccos-.

Значение Л определяю г из (4.27) с помощью первою закона коммутации: при t = 0+ ((0+) = i(0 ) = О и

О = -!ып(\/ А,

Из анализа (4.28) вытекает, что характер переходного процесса зависит от ф и ф. На рис. 4.4,6 изображены графики мгЕЮвенных значений напряжения, установившегося, свободного и полного токов при включении цепи рис. 4.4. а. Следует отметить, что если в момент включения прн t = 0+. \[f - ф = = 0, или ф = ф то принужденный ток равен нулю, поэтому свободный ток ие возникает и в цепи после включения сразу наступает установившийся режим.

4.5. ОТКЛЮЧЕНИЕ КАТУШКИ С г, i ОТ СЕТИ С ПОСТОЯННЫМ НАПРЯЖЕНИЕМ

Допустим, что до отключения в цепи рис. 4.5, а был установившийся ток / = Ь/г и энер ия магнитного поля катушки составляла

Казалось бы, после размыкания выключателя ток до.чжен мгновенно прекратиться. Однако на основании перно! о закона комму laiiHH при ( = 0+ ток сохраняет свое прежнее значение.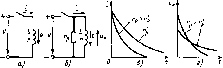

Рнс, 4.5. Отключеине иепи г, L (а) от сети постоянного тока: без разрядного резистора (а), с разрядным резистором {6); зааиси-мости [(() (в) и u£,(0 (г) при отключении цепи г, L с разрядным резистором

Возникает как будто несоответствие: цепь разомкнута, тог есть. В действительности прн размыкании выключателя происходит следующее. Ток уменьшается, н в катушке индуктируется значительная ЭДС. При этом напряжение между контактами вык-тючателя, равное сумме напряжения сетн и ЭДС самоиндукции, пробивает воздушный промежуток между контактами - возникает электрическая дуга и электрическая цепь оказывается замкнутой. По мере увеличения расстояния между контактами сопротивление дуги возрастает, ток и ЭДС уменьшаются н цепь оказывается разомкнутой. За время переходного процесса энергня магцитиого поля катушкн выделяется в виде теплоты в электрической дуге и сопротивлени ка1у1ики.

Переходный процесс в этом случае получается довольно сложным вследствие того, что сопротивление дуги нелиисйпое и изменяется во времени (ei о анализ выходит за рамки даинсв-о учебного пособия).

Отключение цепи с индуктивное i ью вызывает обгоранне контактов размыкающего устройства н появление значительных ЭДС и напряжения на-выводах катушки, превышаю-ших в несколько раз напряжение сети (это может привести к пробою изоляции катушкн).

Во избежание этого в силовых цепях, обладающих значительной индуктивностью (обмотки возбуждения генераторов и двигателей постоянного тока, снпхрОЕншх двигателей, магнитных плит и т. п.). параллельно обмоткам включают разрядные резисторы (рис. 4.5,6).

В этом случае после отключения выключателя катушка индуктивности (V. L) оказывается замкнутой на разрядное сопротивление Гр. Ток в цепи будет убывать значнтелыю медленнее. По этой причине значение возннкаюшей ЭДС будет суишстиен-но меньше, чем без разрядного резистора, н возникшая алабая

дуга исчезает почти мгновенно. В последующих рассуждениях и выводах предполагается, что дуга между контактами не возникает и цепь размыкается мгновенно.

Уравнение цепи, составлешше до второму закону Кирхгофа,

имеет вид ,.

e = i(r-hfp), (4-29)

Заменив е в (4.29), получим

Ldijdl + i (г + Гр) = 0.

(4.30)

Решением дифференциального уравнения будет выражение iAe\ (4.31)

Из характеристического уравнения pL-\-{t + r = q определяют покща1ель степени р:

Г + Гр 1

---Т- Т

Подставив это выражение в (431), получим

тдс TL/I/--I-Гр) - постояипзя времени цепи.

Значение А определяют из начальных условий иа основании первого закона коммутации; при t = 0

i = I = U/r и А=и/г. Выражение тока в цепн имеет вид

(4.32)

Подставив в (4.29) значсвие i из (4.32), получим ЭДС

Напряжение иа выводах катушки равно напряжению на разрядном резисторе:

в начальный момент при i=0 6

(4.33) 163

(4.34)

Из выражений (4.33) и (4.34) вытекает, что начальные значения €на>, И нда, зависят ОТ сопротивлсиия рззрядного рсзистора. При больших значениях Гр оин MOiyi оказаться чрезмерно большими и опасными дня изоляции установки.

Иа рис. 4,5.в изображены графики и u(i) катушки после отключения цепи дтя двух значений Гр, Гр > гр.

На практике обычно выбирают Гр в 4-8 раз больше собственного сопротивления обмотки индуктивной катушкн:

- , = (48) (4.35)

Пример 4.2. Определить начальные значения ЭДС самоиндукции и напряжения на катушке прн отключении цени, изображенной на рис. 4.5,6, j,Ta двух значений г. а) Гр = 4г; б) Гр=20. Параметры це-пи: г= 1[Х) Ом. t) =400 В.

Решение. Начальное значение тока в катушке / = 07 = 400/100 = 4 А.

Начальные значения ЭДС.

а £ 84 = 11аЛ + р) = 4(100-1-4-100) = 2000 В;

и, .ач-Wp = 4-400= 1600 В;

б) = (г 4- Гр) = 4 (100 + 20.100) = 8400 В:

(iha4 = Wp= 4-20 100 = 8000 В.

4.6. ПЕРЕХОДНЫЙ ПРОЦЕСС В ЦЕПИ ПРИ ИЗМЕНЕНИИ ЕЕ ПАРАМЕТРОВ

Рассмотрим переходный процесс в цепи, вызванный изменением ее параметров, например изменением сопротивления в одном нз 5частков цепн, изображенной на рнс. 4.6, а.

До замыкания выключателя ток в цепи

После замыкзЕшя выключателя

Таким образом, при замыкании выключателя в цепи возникает переходный процесс, в течение которого ток изменяется от 1 цо 1у.

Рис. 4.6. Зависимости /(г], eij) (о) при изменении параметров пепи г. L (а)

Уравнение цепи, составленное по второму закону Кирхгофа, имеет вид

Ldijdt ir= V. (4.36)

Решением уравнения без правой части (для свобощюго тока) L<iu/(il-Ы> = 0

будет выражение

Из харак-геристического уравнения -t- г = О определяют показатель степени р:

Оощнй ток в цепн

где ijo, = Jjcr = При I = О,

i = уст + Ае\

(4.37)

и и

После подстановки А в (4.37) получим уравнение для тока 1 переходный период:

(4.38)

Подставив i из (4.38) в (4.36), получим выражение ЭДС

(4.39)

На рис. 4.6, б изображены графики / и е переходного про-цесся в цепи рис. 4.6, а

Пример 4.3. Определить начальное зттченне ЭДС е в индуктивности цени, и1с5раженной на рнс. 4.6, а. при замыкании выключатс.тя.