На рис. 4.2,6 изображены графики тока и ЭДС e{i) при включении цепн рис. 4:2, а.

Легко показать, что касательная, проведенная к кривой тока в начале координат, отсекает отрезок на линии установившегося значения тока, равный постоянной времени цепи Т. Действительно, как вьнекает из выражения (4.5), при t = 0 и t = 0

di/dt = U/L=tgoi.

Из рис. 4.2,6

tga = v.,/7:

После подстановки получим

U/L = ]y/T=U/rT,

L/r.

(4.11)

Постоянная времени характеризует темп нарастания тока в цепи. Она зависи! еолько от параметров цепн и позволяет без расчета и постросння графиков оцени1Ь длительность переходного процесса.

Длительность переходного процесса, как видно из выражений (4.9) и (4.10), теоретически равна бесконечности. Практически же

при 1=ЗТ , = 0,951 ;

при f = 4T i = 0,98/, ;

при i = 5T ; = 0,993/, .

Обычно ичи1аюг, что длительность переходного процесса составляет

(=(Зн-4)Т.

В практике расчет<ж п(тоодных процессов в эшяп-рнчоапн цепях используют известный метод решения линейных диффе-{ нциальных уравнений с правой частью. Результат решения дифферепциазьного уравнения равен сумме частного решения неоднородного дйффереттциалыюго уравнения и общего одяо-родагого уравнения (когда правая часгь исходного уравнения равна нулю). Дггя использования этого метода действ тельиъзй (переходный) ток в ветви в соогасгстмга с уравнением <4.9) представляют как сумму двух сосгаилшощнк

i = iy + ic . (4.12)

где - установившийся ток, т. е. ток, котсфый устанавливается в цепн после окончания переходного процесса; - сво-бошый ток - ток, действующий только в течение времени переходного процесса.

Выразив в дифференциальном уравнении (4.5) ток через две составлиющие, палучим

Так как в установившемся режиме ia - О, то уравнение (4,13) приобретает вид

14.14)

Ток в установившемся режиме есть ведичнна постояииая,

и его производная

-.0.

Тогда нз (4.14) следует, что

i = Vir = I .

Вычитая (4.14) из (4.13), получим дифференциальное >равис-ние лля свободного тока

LdiJdt + ! = 0. (415)

Решением этого уравнения является выражение

L.= Ae , (4.16)

где р - кореш, характеристического уравнения pL+ г - О, г 1

(4.17)

Таким образом.

Действительный ток в цепи в переходном режиме

i - i, + 4е-/т= VIr + Ае-Ч. (418)

Значение А определяют из начальных условий: при t = 0 i(O) = i(0 ) = 0 и

Л = - и/г.

Подставив значение А в (4.18), получим такое же уравнение для тока D цепн, как и при решении дифференциального уравнения методом разделения переменных:

и и

i = -----e-fTI,-I e-n.

Из изложенною вытекает, что установившийся ток определяется с помощью закона Ома, как в этом случае, нли в раз-ве]вленнык цепях с помощью законов К1фхгофа, а свободный - из решения исходного дифференциального уравнения без правой части.

4.3. ПОДКЛЮЧЕНИЕ РАЗВЕТВЛЕННОЙ ЦЕПИ

С РЕЗИСТИВНЫМ И ИНДУКТИВНЫМ ЭЛЕМЕНТАМИ

К СЕТИ С ПОСТОЯННЫМ НАПРЯЖЕНИЕМ

После включения выключателя (рис. 4.3, й) в цепи возникает переходный процесс. Поскольку в цепи действуют три тока, необходимо составить три уравнения по законам Кирхгофа:

/-Ч +12-, (4.19)

e = ir + ijrj - U; (4.20)

? = i,r,-.,r, (4.21)

Совместное решение уравнений относительно тока дает

Выразив е через - L di-Jdt, получим дифферещнатьное уравнение

b±Lj!jll±l2LlIh\i=L, (4.2Са) гг dt \ гг, / <

Решением дифференциального уравнения без правой части (для свободного тока) будет выражение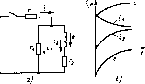

Рис. 4J Зависимости i(r), ii (г), izit), e{t) (6) нри включении разветвленной цели г, L (а) в сеть постоянного тока, эквввалеитная относительно постоянной времени Т цепь (в)

Значение р определяют из характеристического уравнения

Г, + г ГзГ, + г,г + гг.

Г2Г1 + ГдГ + rrj

где г-

- постоянная времени цепи.

Как видно, постоянная времени цепи определяется параметрами всех ее элементов, а не только ветви с индуктивностью. Ток [2 в переходный период будет равен

Принужденный ток определяют из выражения (4.21а), в котором при t = со dijdi = О и

Г,Г, +Г2Г + ГГ,

Таким образом.

Значение А определяют с помощью первого закона коммутации: при t = 0 ( 2(0.) = /2(0-) = и

А = -hycr.

Ток 12 в переходный период будет равен

2 =hy-l2r.e-r

(4.22)

Подставив в (4.21) значение тока и его производную, получим выражение для тока Il:

. = -(/, -4.Jf- , (4.23)

; I -

После подстановки и i, в (4.19) найдем выражение для тока i:

(4.24)

i = ,=r-(f,c-,.Je-/r

Выражение ЭДС р можно получить из (4.21) после подстановки в него вместо ij и ii их значении нз (4.23) и (4.22):

(4.25)

Па рис. 4.3,6 нзображмы графики токов i{t), ii(t), lalO и ЭДС £(0 при включении цепи рис. 4.3,а (при г-Гз).

Следует обратить внимание иа то, что расчет токов в ветвях разветвленных цепей с одним накопителем, например катушкой с индуктивностью L, можно значительно упростить и выполнить без составления н решения уравнений (4.19) - (421). Это можно сделать, если предюригельпо определить постоянную времени Г цепи с помощью эквивалентной схемы (рис. 4.3, б). Для этого все резистивные элементы заменить одним эквивалеитным относительно индуктивного элемеггга. Цепь, эквивалентная рис. 4.3, о, изображени на рис 4.3, в. Цепь эквивалентна только в отношении постоянной времени Т.

Эквивалентное сопротивление цепа составит

гг. Г2Г + Г2Г, +ГГ,

r+ri r + r,

ПостояпЕшя времени эквивалентной цепи

г-уГ + г,с, -- гг.

имеет то же зиачеине, что и реальной.

Зная постоянную времени н определив начальные н установившиеся знадагая токов в ветвях, легко написать их выражения для переходното процесса в цеди. Own будут такими же, как и ранее полученные из решения системы уравнений.

Пример 4.1. Огфедслнть началынж я установившиеся значения токов 1, i\. ij, ЭДС е, постоянную времени и длительность пере)!одно-о процесса при включении цепи рис, 43, а в сеть постоянного тока. Параметры цепи: г = 2000 Ом, г, = = 3000 Ом, V = Ш В, L=0,1 Гн.

Решение, Начальные значения токов:

/,. о- = = 0.04 А.

-зн., , И.ч 2000 + 3 10

Начальное значение ЭДС

£,т-11щч1-0>[М-3< 0.120 В.

Установившиеся значения токов и ЭДС:

V 200 200

3500

= 0,057 А:

СТ--

3000 + 3000 200 - 0.057-2000 3000

200 - 0,057.2000

3000 f, = 0.

0,0285- А; 5 0,0285 А;

Постоянная времени контура

Цг,-ьг) 0,1 (3000-ь 2000)

3000 - 30003000-20003000-2000

Длнтелы[ость переходного процесса

1 =4Т=9,6-1 с-