Мощности установки hi приемников и батареи кондеисаторов P = J>=I8,7 кВт; Х = Р/со5ф= 1У.68 кВ А; 6 = ys = 6,13 кзар.

Линейные токи установки из 1гриемников и батареи конденсаторов, мощность и линейные токи батареи конденсаторов

/ = ;; = y/l/3L;,= 5l.7 А; - б - G= 15,67 квяр, ,л = е. 3(/л=41.2А. Фазные юки и сопротивление фазы батареи конденсаторов /.,<t = к.л/! = 20,8 А; х, 4, = U/l = /лДк,ф = 10,58 Ом. Емкость одной фазы и всей батареи конденсаторов

Ск.ф= 1/27[/х.ф=30 мкФ; (Г = ЗС.,ф = 90 мкФ.

Векторная диаграмма депи рис. 3.18, а приведена на рис. 3.18, б. На диаграмме показаны только тс гоки, которые определяют ток 1т. е. / и а также токи, определяющие ток (т. е. iah и /.J.

ЗЛ. ВЛИЯНИЕ СОПРОТИВЛЕНИЙ ПРОВОДОВ СЕТИ НА НАПРЯЖЕН>1Я ПРИЕМНИКОВ. ПОСЛЕДОВАТЕЛЬНОСТЬ РАСЧЕТА.

При изменении числа приемников, подклю1е1[ных к трехфазной сети, изменяются падения нанряження в сопротивлениях проводов сетн, в peiyjfbTaTe чего напряжения приемников не остаются неизменными.

Прн симметричной нагрузке и равенстве сопротивлений проводов сети падения напряжения получаются одинаковыми, н результате чего фааные и линейные напряжения приемников оказываются симме-тричньпяи. В отличие от этого при несимметрипюй нагрузке падения напряжения в сопротивлениях проводов сети получаются неодинаковыми, что приводит к несиммстрин фазных и линейных напряжений приемников.

Длн уменьшения колебаний и степени 1[есимметрии напряжения приемников площадь поперечного сечения проводов электрических сетей выбирают НС только по нагреванию, но и по допустимой поте напряжения. Учитывая относительно нс5ольш>ю потерю напряжения в сопротивлениях проводов при норма.1ыюй их загрузке, часто принимают линейные и фазные напряжения приемников симметричными даже при несимметричной нагрузке.

Рассмотрим последоватсльвость расчета трсхфа ных цепей с учетом сопротивлений проводов, считая, что заданы симметричные напряжения в начале элек1рическ< сети.

При симметричной нагрузке и соединении приемника звездой следует определить эквивалентные фазные сопротиилепив, включающие в себя сопротивления приемника и проводов. После этого нетрудно опред&тнтк фазные токи, а затем фазные напряжения приемникл. Длн определения линейных напряжений приемника стедуст воспользоваться формулой (3.9).

Если при соединетЕии звездой нагрузка несимметричная, необходимо решать задачу в комплексной форме. Прн этом HeJrecoo6pa3Ho использовать метод узлового напряжения. Определив напряжение между нейральными точками N, к N (см. рис. 3.3 и 3.7) трехфазного источника и приемников, можно найти фазные токи и напряжения, а затем -линейные напряжения.

Прн симметричной на1рузке и соединении треугольником следует, используя комплексный метод, найти активное и реактивное сопротивления эквивалентной звезды. Далее задача решается в порядке, изложенном вьпие для соединения звездой. Фазные токи при соединении треугольником определяют по формуле (3.19).

Если при соединении (реую.тьннком нагрузка несимметричная, то следует воспользоваться комплексным методом и решать задачу в такой последовательности: преобразовать треугольник сопротивлений в эквивалентную звезду; определить эквивалентные сопротивлении, включающие в себя сопротивления эквиваленгной звезды и проводов; преобразовйпь гнезду с эквивалентными сопротивлениями в эквивалентный треугольник; с помощью закона Ома определить фазные токи, а зная их и используя выражения (3.17), найтн линейные токн: в заданной цепи с соединением приемников треугольником определить по второму закону Кирхгофа фазные напряжения приемников, после чего по закону Ома вычислить их фазные токи.

Глава четвертая

ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ

4.1. ОБЩИЕ ВОПРОСЫ И ОПРЕДЕЛЕНИЯ

Прог(ессы, протекающие в электромагнитах, механических и тепловых системах при переходе из ozworo устанокившегося (стационарного) состояния к другому, при котором энергия системы (соответственно энергия электрического и магнитного полей, кинетическая энергия и тепловая э]1ергня и обуатовлн-вающие их величины - напряжение, ток, скорость и температура) изменяется, называются переходными или иеусхановивши-мися процессами.

Процесс перехода от одного }сгановившсгося состояния к другому протекает не мгновенно (скачком), а постепенно в те-

чение определенного времени в силу того, что энергия скачком изменяться не может и. следовательно, не может изменяться скачком обусловливающая ее величина. Если предположить, что энергия изменится мгновенно за время г - 0. то мощность, необходимая для этого.

Рис. 4.1. Зависимости Ut), ф) (6) при подключении идеальной жа-(ушки с индуктивностью L (а) к сети с постоянным валряжением

оказалась бы равной бесконечности, а источников е бесконечной мощностью в природе не существует.

В электрических цепях, содержащих в общем случае рези-стивиый, индуктииный и емкостный эдемепты, переходный процесс возникает лрн включении, вырслючеиии и изменении параметров цепн. Такие действия в общем случае называют коммутащ1ей электрической цепи или просто коммутащ1ей. После коммутации изменяется энергия индуктивного Wi = IL/2 и емкосгною Wc = CV/2 элементов. Поскольку энергия мгновенно изменяться не может. следовательно, ие может изменяться мгновенно ток в индуктивности и иапряжсниЕ иа емкости. Из этого вытекают два важных положения (их называют зако-нами коммутации), без знания которых невозможно рассчитыватьи анализировать перехохщые процессы в элск i рических цепях.

Первый закон коммутации; ток в ветви с индуктивностью после коммутации iO) (включепне, отключение, изменение параметров цепи) при / = имеет то же значение, что и до коммутации t,.(0 ):

Второй закон коммутации: напряжение иа емкости после яоммутации Мс(0+) при 1 = 0+ имеет такое же значение, что и до коммутации:

с(0,) = с(О-).

Аналогичные законы есть и в механике, например оторость тела (массы) после начала действия силы прн t = 0+ равна скорости до начала действия силы.

При расчетах переходных процеесо используют так называемые начальные значения тока н напряжения а ветвях цепи, которые в совокупности с закоиа.мя коммутации позволяют определить постояш1Ь]е интегрирования. Под начальными значениями тока и няпряжеиия понимают нх значения до коммутации при t = О,. Необходимо отмегить, что ток в ветви толь-

ко с одним резистивньгм элементом изменяется скачком по той причине, чю энергия в нем не накаплщастся, а вес время преобразуется необратимо а теплоту и ее значение w = uii пропорционально времена, а мощность p = dw,dl = ui имеет конечное значение.

Общность переходньо! процессов в механических системах и электрических цепях можно проследить ня примере протекания процесса при действии силы F на тело с массой т н при включении индуктивного элемента с индуктивностью £,к источнику с постоянным напряжением.

Известно, что сила, действующая на тело, связана с массой и ускорением законом Ньютона

F = mdvjdt,

(4.1)

откуда следует, что постоянно действующая сила вызывает движение тела с ускорением, равным

dvfdtF/m.

(4.2)

Скачкообразное изменение скорости гела, когда 4v/dt = оо, невозможно, так как сила может иметь конечное, а не бесконечно большое значение.

При включении идеальной катушки (z = 0) с индуктивностью 1,(рис- 4.1,0) под действием напряжения сети в ней возникает ток и ЭДС самоиндукции. Идеальные индуктивности существуют реально - это обмотки электромагнитных исследовательских устройств элементарных час1иц. вылолненные из сверхпроводящих материалов, сопротивление которых при кр1югенных температурах равно нулю.

И* кыражения, составленного по вт<му закону Кирхгофа,

[/ = - e = L di/dt (4.3)

вытекает, что скорость нарастания тока равна di/dt = U(L,

(4.4) 151

Сопоставляя (41) и (4.3), можно заключить, что индуктивность по своему действию аналогична массе в механической системе.

Из выражения (4.4) следует, что при определенном конечном значении U скорость изменения тока в индуктивности имеет определенное конечное значение. На рис. 4.1,6 изображены графики тока i и ЭДС с при включении пепи но рис. 4.1. а.

В системах автома1Ического управления часто происходит нарушение установившихся режимов и они практически работают в условиях переходного режима. В большинстве систем автоматического управления используются электротехнические устройства, поэтому необходимо рассмотреть переходные процессы хотя бы в простейших электрических цепях.

Рис. 4,2. Зависимости /(;), e(t) при nonKjrK)4CHHH катушки г. L . (я) к сети с постоянным напряжением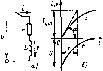

{4.6)

где Г= L/r - электромагнитная постоянная времени, с.

В результате решения дифференциального уравнения (4.6) методом разделения переменных получим

(4.7)

Выражение 74.7) в показательной форме будет иметь вид

4Л. ПОДКЛЮЧЕНИЕ КАТУШКИ С г. L К СЕТИ С ПОСТОЯННЫМ НАПРЯЖЕНИЕМ

Схема замещения реальной катушки (рнс. 4.2, а) представляет собой последовательно соединенные решстивный г и индуктивный L элементы.

После включения выключателя (рис. 4.2, а) в цепи возникают юк и ЭДС самоиндукции. Уравнение для цепи, составленное по второму закону Кирхгофа, имеет вид

е = 1г - и.

Выразив в уравнении е через

е = -Ldi/dt,

получим

€= -Ldi/dt -ir - и. (4.5>

Разделив почленно (4.5) на г, получим Ldi , и г dt ~ г

--/ = Лс-/т;

(4.S)

где Л - постоянная иитегр1фОваиия.

Постоянную интегрирования определяют на основании первого закона коммутации.

Прн ( = 0 i(0)=i{0 ) = 0;

А = и/г.

После подстановки в (4.8) значения А и решения его оттюси-тельпо i получим уравнение тока в цепи г, L

(4.9)

где /уст = Ufr - уста]ювившийся ток в цепи после окончания переходного процесса.

Подставив в (4.5) значение тока из (4.9), получим ураиие-ние ЭДС самоиндукции е, возникающей в индуктивности: e--Ve-\ (4.10)