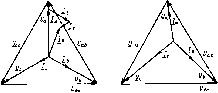Рис. 3.10. Векторная диаграмма при соединении приемников звездой в случае несимметричной нагрузки и при наличии нейтрального провода

Рис. ЗЛ Векторная диафамма при соединении приемников звездой в случае несимметричной нагрузки и обрыве нейтрального провода

диаграмм отчетливо видны последствия обрыва нейтрального провода.

Необходимость нейтрального провода становится особенно очевидной, если представить себе, что при отсутствии нейтрального провода отключили все приемники, например, фаз а и Ь. Очевидно, напря-женне фазы с при этом окажется равным нулю, так как фаза с окажется также отключенной. Если вообразить, чю имеется всего лишь одип од1юфазный приемник, рассчитанный на напряжение [/л з, то прн отсутствии нейтрального провода ею попросту было бы некуда включить.

Для повышения надежности соединения приемников с источником с помощью нейтрального провода в цепи последнего не ставят вьшлючатслсй и даже защитных устройств, например предохранителей.

Фазные токи, у1лы сдвига фаз между фазньиу1И напряжениями н тока.мн, а также фазные мощности прн песимметрнчной нагрузке в цепи с нейтральным проводом будут в общем случае различными. Все они могут быть определены по приведенным ранее формулам (3.12) Для определения мощностей всех фаз следует воспользоваться выражениями

Р-Р + Рь + Рс Q = Q, + Q, + Qc- (3-15}

Очевидно, формулы (3.13) и (3.14) не пригодны для определения мощностей при несимме[ричной нагрузке.

Если требуется определить ток 1 нейтрального провода, то следует решать -Задачу комплексным методом. Можно также огфеделить ток i. по векторной диаграмме, которая, естественно, должна быть построена в масштабе.

При решении задачи в комплексной форме необходимо прежде всего выразить в комплексной форме полные сопротивления фаз и фазные напряжения. После этого нетрудно найти комплексные выражения фазных токов. Например, комплексное выражение тока / будет равно = V/Zj,.

Комплексное значение тока в нейтральном проводе определяют по формуле (3.10).

Комплексным методом можно воспользоваться и для определения фазных мощностей. Так, мощности фазы а будут равны

= Р - Re Q = Im S , S = \/p; hQJ.

Пример 3.2. В электрической цепи рис. 3.7 линейные напряжения С/ , = 220 В. В фазе а включено паралчельно 20 ламп, в фазе b - ]0 ламп, в фазе С - 5 ламп. Номинальное папряжепне и мощность каждой лампы равны С/ о -127В, = 100 Вт. Определи ь фазные токи, ток каждой лампы и ток нейтрального провода

Решение. Учитывая, что лампы имеют только активное сопротивление, из формулы мощности найдем номинальный ток ламны, а но закону Ома - сопротивление лампы-

/но - Рном/Снсм = 100/127 0,79 А, ном = ном = 127/0,79 161 Ом.

Зная сопротивление лампы и чиаю jihmh в каждой фа1е, нетрудно оирелелить сопротивление фаз, а затем фазные токи:

г 161/20 8.05 Ом. ** 161/10 = 16,1 Ом,

161/5 = 32,2 Ом, = UJr =,127/8,05 х 15,8 А,

Sf, 7,9 А, 1, 3,95 Л.

Так как при (7 = 220 В напряжение на лампах равно их номинальному напряжению, т. е. 127 В, то каждая лампа будет потреблять ток, равный номинальному, т. е. 0,79 А.

Для определения юка в ней1ральном проводе решим задачу комплексным методом. Так как при сделапиыи ранее допущениях комплексные значения фазных напряжений приемника равны комплексным значениям соответствующих ЭДС [см (3.2)]. то

С/С/,-127 В. C/cos(-2n/3)-l-/C;j5in(-2n/3)= ~63,5->l]0 В. = cos ( - 47!/3) -I- sin { - 4rt/3) = - 63,5 -Ь 110 В.

Комплексные значения Z, = 16,1 Ом. Z, = 32,2 Ом.

тзных сопротиаленин. Z = 8,05Om,

Комплексные значения токов и действующее : трального провода:

i = l/,/Z * 15,8 А; /ь (-3.94-/6,83) Л; /. (-1.97+У3.41) А;

/ -/ -1-/ь + /, {9,89-j3.42)A; /д-/9.89 + 3,42 10.5 А. Векторная диаграмма к примеру 3.2 дана на рис. 3.10.

3.5. СОЕДИНЕНИЕ ПРИЕМНИКОВ ТРЕУГОЛЬНИКОМ

Как видно из схемы рис. 3.12. каждая фаза приемника при соединении треугольником подключена к двум линейным проводам. Поэтому независимо от значения и характера сопротивлений приемника каждое фазное напряжение равно соответствующему линейному напряжению:

U=V,. (3.16)

FcTH не учитывать сопротинлений проводов сети, то напряжения приемника следует считать равными линейным напряжениям HCTOHHiuca.

На основании схемы рис 3.12 и выражения (3.16) можно сделать вывод о том, что соединение треугольником следует применять тогда, когда каждая фаза трехфазного приемника или опюфазиые приемникн рассчитаны иа напряжение, равное номинальному линейному напряжению сети.

Фазные токи 1, 1 и 7 в общем случае не равны линейным токам /(, и 1. Применяя первый закон Кирхгофа к узловым точкам а, & и с, мож1Ю получить следующие соотношения между линейными и фазными точками:

L=Lb~L.. L, = lu-U. L-L.-lb.- (3.17)

Используя указашше соотношения н имея векторы фазных токов, нетрудно построить векторы линейных токов.

3.S.!, Симмевричная ншрузка. В отношении любой фазы справедливы вес фсфмулы, полученные ранее для однофазных цепей, например

(3.18)

Рнс. 3.12. Соеди приемника ipeyro.i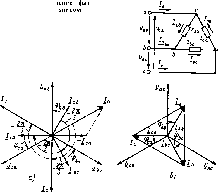

Рис. 3.13. Векторные лиа1ра.ммы при соединении пр] угольником в случае симметричной нагрузки

Очевидно, при симметричной нагрузке

= ф = ф< = фф; Р., =П. =Р,. =Pti

Векторная диаграмма фазных (линейных) напряжений, а также фазных токов при симметричной акгивно-индуктивпой HdipyjKe приведена на рис. 3.13,я. Там же в соответствии с выражениями (3.17) построены векторы линейных токов. Следует обратить внимание иа то, что при изображении векторных диа-гра.мм в случае соединения треугольником вектор линейного напряжения [/j принято направлять вертикально вверх.

Из приведенных выражений и векторной диаграммы следует, что нрн симметричной нагрузке существуют симметричные системы фазных и линейных токов.

Векторы линейных токов чаще изображают соединяющими векторы соответствующих фазных токов, как показано на

рнс. 3.13, б. На основании векторной диаграммы рис. 3.13, о -= 2/sin60° =],/з/ ь- Такое же соо1ношение сущесгвуст между любыми другими фазными и линейными токами. Поэтому можно написать, что при симистричной нагрузке вообще /, = Л/ф. (3.19)

Для определения мощностей трехфазного приемника прн симметричной нагру:5ке можно воспользоваться получеппымн ранее формулами (3.13) и (3.14).

Пример 3.3. К трехфазной сети с линейкы.ми напряжениями Гл = 220 В должен быть подключен трехфазный приемник, каждая фаза которого рассчитана на напряжение 220 В и содержит активное сопротивление Гф=-8,б5 0м, а также индуктивное сопротивление Хф = = 5 Ом, соединенные последовательно.

Определить фазные и линейные токи, углы сдвига фаз между фазными напряжениями и токами, а также мощности.

Решение. Так как каждая из фаз приемника рассчитана на напряжение, равное линейному напряжению трехфазной сети, фазы приемника должны быть соединены треугольником (см. рис. 3 12).

Полные сопротивления фаз, фазные и линейные токи: Ч = У4+4=10 /йиф/7ф = 22 А, /. = i/зГф = 38 А.

Углы сдвига фаз межл> напряжениями и токами

Полная активная и реактивная мошностн приемника и любой фазы

S = l/31/л/л = 4730 В А = 4,73 кВ А; S = S/ * 1576 В-А 5. 1,58 кВ. А; PS eos (рф = Sj-ф/гф 4100 Вт = 4,1 кВт; Рф -Р/3 % 1366Вт 1,37 кВт; Q = S sm фф = Sxz 2365 вар =t 2,36 квар; Оф = 6/3 788 вар = 0,788 квар Векторные диаграммы приемника приведены иа рис. 3.13.

3.5.2. Несиммет{№чная нагрузка. Как и при соединении звездой, в случае соединения треугольником однофазные прнемин-ки делят на три примерно равные в отношении мощности группы. Каждая группа подключается к двум проводам, между которьпли имеется напряжение, от.1ичающееся по фазе от двух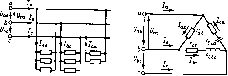

Рис. 3.14. К вопросу о соединении однофачнык приемников треугольником

Рис. 3.15. Схема цепи к прн-мер> 3.4

других напряжений сети (рис. 3.14). В пределах каждой группы приемники соединяются параллелыю.

После замены приемников каждой фазы одним приемником с эквивалентным сопротивлением и соответствующего нх расположения получим схему, приведенную на рнс. 3.12.

Фазиые токи, углы сдвига фаз между фазными напряжениями и тока.ми, а 1акже фазные мощности можно определить по формулам (3.18). При несимметричной нагрузке фазные токи, углы сдви1а фаз и фазные мощности будут в общем случае различными. Векторная диаграмма для случая, когда в фазе ah имейся активная нагрузка, в фазе be - активио-индуктивная, а в фазе са - активно-емкоетиая (рнс. 3.15), приведена на рис. 3 16. Построение векторов линейных токов произведено в соответствии с выражениями (3.17).

Для определения мощностей всех фаз следует пользоваться формулами

Р = Кь + Ры + Р.., Q-Qab + Qb.+Q.. (3.20)

Формулы (3.13) и (3.14), полученные ранее для симметричной нагрузки, не нриюдны для определения мощностей при несимметричной нагрузке.

Если кроме фазных токов требуется определить линейные токи, задачу следует решать в комплексной форме. Для этой же hCjih можно воспользоваться векторной диаграммой.

Нри решении задачи в комплексной форме необходимо прежде всего выразить в комплексной форме фазные напряжения, а также полные сопротивления фаз. Когда это сделано, нетрудно по закону Ома определить фазные токи. Например, комплексное выражение тока 1 будет

(3.21) 141