Напряжение как это следует иъ уравнения Кирх ифа.

Из векторной диатраммы рис. 2,22,6 видно, что зЕтачение напряжения при изменении сопротивления резистора г ociaciCH неи1менным, а его фаза изменяется.

2.16. РАСЧЕТ СИНУСОИДАЛЬНЫХ ЦЕПЕЙ

С ИСПОЛЬЗОВАНИЕМ КОМПЛЕКСНЫХ ЧИСЕЛ

В практике расчета цепей переменного тока широко используются комплексные числа

Комплексными числами и векторами на комплексной плоскости изображаются изменяющиеся синусоидально ЭДС, юк и напряжение, а также полные сопротивление н проводимость, полная мошность и некоторые другие параметры цепи.

Использование комплексных чисел при расчете электрических цепей переменного тока позволяет за,менить графические лейс1вия над векторами алгебраическими действиями над комплексными числами Кроме того, при использовании комплексных чисел возникает полная аналогия записей уравнений по законам Ома и Кирхгофа и,методов pac4eia цепей переменного тока с цеггями постоянного тока,

В тпик постоянного тока в уравнения входят действительные значения Е. U, I, г. в цепях переменного тока - комплексные значения U, £, L, Z-

Как известно нз курса матема1ики, комплексное число C~a+jb, где j = у -I. имеет гве составляюшие - лейевигельную а и мнимую Ь, которые являютсх координатами точки на комплексной плоскости (рис, 2 23, а). Комплексная плоскость представляет собой прямоугольную систему координат. По одной оси. называемой действительной и обозначаемой ! , ( - 1, откладывается действительная составляющан комплекса (я), по другой оси, нагываемой мнимой и обозначаемой (+Д (-Д-мнима* составинющам комплекса (Ь).

Комплексное числи обозначается чертой год буквенным обозпаче-Htieu. Комплексное число может быть предстаолено вектором, длина которого является модулем комплекса, а положение определяется углом а отпоснте.п.ио положительной действительной оси кпмплскс-iroii плоскости (рис. 2,23, о).

Выразив а а Ь черех MOjiynh (длину вектора) и угол, можно записать комплексное число в григонометрической форме: С - а + jb = ccoia +JC sin а,

где с\/а - - модуль комплексного числа 106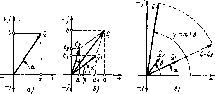

Рис. 123 Изображение комплексного числа на комплекспон плоскости (а), стожсние (б) и умножение (в) комплексов

Согласно формуле Эйлера комшгексное число можно записать н показательной форме:

С = сС\

1ле (?-основание натуральны.х логарифмов

Рассмотрим основные геометрические операции над векторами и алгебраические действия над комплексными числами, их изображаю-[цими

Сложение дбух комплексов можно произвести аналитически: Г -Г, + Г, +;Ь,) -f К jb,) = {и, -f а,) -t-;(b, + b,) = а +}Ь

или графически по правилу сложения векторов (рис. 2.23,6).

Произведение двух комплексных чисел, изображающих векторы Г, и Сг, являека ком1шексиым числом, которому соответствует век-гор С-

Вектор комплекса произведения двух векторов имеет длину, рав ную произведению модулей, а его положение относнтелыю действительной положительной оси определяется суммой углов векторов сомножителей (рис. 2.23, в).

Новый вектор, возникающий а результате умножения комплексного числа £ =г - на j или - f, имее! lui ж; MOnyiib с, ио повернут па 90 oiHoenrwrbHo исходного вектора: в одном случае - против часовой стрелки, в другом - по часовой стрелке.

Действительно, векторы +; и -j в показательной форме могут быть записаны следующим образом:

В результате деления двух комнлекеныл ччсея иолучастя

модуль которого равен частному от деления модулей, а >гол - раию-сти >глов исходных комплексов.

2.17. ИЗОБРАЖЕНИЕ НАПРЯЖЕНИЙ И ТОКОВ КОМПЛЕКСНЫМИ ЧИСЛАМИ И ВЕКТОРАМИ НА КОМПЛЕКСНОЙ ПЛОСКОСТИ

Запишем комплексное чисю в виде

Jm = д* - COS а + sin 7.

Допустим, 410 вектор комплексного числа срдиается с постоянной угловой частотой ш и уюл а - (о; + 4f. Тогда

Z e° - cos(w( +iif)+j7 sin{co/ +

Слагаемое / cos (cot + ijf) представляет собой дейсггвитель-ную часть комплексного числа и обозначается

/ cos (cof + lif) = ReI e* -*\

Слагаемое / sin(o)r -f-ф) есть коэффициент при мнимой части комплексного числа и обозиачается

Легко видеть, что коэффициент при мнимой части комплексного числа представляет собой выражение мгновенного значения сннусоидальни!и гока

= / ,sin (cof + ф)

и является проекцией вращающегося вектора на мнимую ось комплексной плоскости

Синусоидально изменяющиеся по времепн величины изображаются на комплексной плоскости для момена времени

f 0. Тогда комплексная амплитуда записывается в виде

де / -комплексная амплитуда; / -ее модуль, а \/- угол между вектором / и действительной осью.

Таким образом, комплексная амплитуда изображает синусоидальный ток на комплексной плоско1:1И для момента вре-viCHH I - 0.

Допустим, что в электрической цепи мгновенные значения напряжения и тока имеют выражения

и Csin (tor + ill,);

Комплексные амплитуды напряжения и тока должны быть записаны в виде

де V и / -соответственно модули комплексных амплитуд напряжения и тока; и ijf, - начальные фазы С, и / относительно действительной оси (углы начальных фаз)

Обычно принято выража1ь в виде комплексных чисел не амплитуды, а действующие значения напряжений и токов-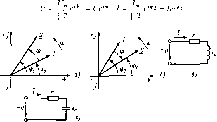

Рнс, 2.24. Нзооражегше напряжения ломплекспон плоскости (я и б) электричес!

гока в виде векторов на цепей (6 и

Если <i>2> векторы напряжения и тока расположены на комплексной плоскости так, как показано на рис. 2.24, д. Напряжение опережает по фазе ток, так как векторы вращаются против часовой стрелки и, следовательно, цепь имеет активно-иидуктивный характер (рис. 2.24,4

При \/2 > Il (рис. 2.24, б) ток опережает по фазе напряжение и цепь имеет активно-емкостный характер (рнс 2,24, г).

2.1в. КОМПЛЕКСНЫЕ ЗНАЧЕНИЯ ПОЛНЫХ СОПРОТИВЛЕНИЙ И ПРОВОДИМОСТЕЙ ЦЕПИ. ЗАКОН ОМА В КОМПЛЕКСНОЙ ФОРМЕ

Разделив комплексное напряжение на комплексный ток, получим комплексное полное аэпротнвление

где Z- и/1 - модуль полного сопротивления; ф - угол сдвига фаз между током и напряжением.

Выразив комплексное значение полного сопротивления в тригонометрической н затем в алгебраической форме, получим;

для цепи с активно-индуктивным характером (рис. 2.24, в% 2 = = Z cos ф -I- /2 sin ф = г + jxi;

для цепи с активно-емкостным характером (рис. 2.24, г),

Z - ze~ = 2С05ф - /г8Шф = г -jxc,

где rzcosip, Xf. = zsinф, Дс 2sinф - соответственно активное, индуктивное и емкостное сопротивления цепи. Закон Ома в комплексной форме:

l = vtz.

где Z = г + jXj для цепи, состоящей из последовательно включенных активного г и индуктивного сопротивлений; Z = г --jXc для цепи, состоящей из последовательно включенных активного г и емкостного х сопротивлений.

Полная проводимость в комплексной форме записывается следующим образом:

для цепи, состоящей из последовательно включенных активного и индуктивного сопротивлений,

Y = J J {r-JXj) г ~JXL

г Xt

ддя цепи, состоящей из последовательно включенных активного и емкостного сопротивлений.

и Z r-jxc z-

где g и b -- соответственно активная и реактивная проводимости цепи.

2.19. ЗАКОНЫ КИРХГОФА В КОМПЛЕКСНОЙ ФОРМЕ

Первый закон Кирхгофа гласит, что алгебраическая сумма мгновенных значений токов в любом узле цепи равна нулю: Si = 0.

Выразив мгновенные значения токов через их комплексные выражения, получим первый закон Кирхгофа в комплексной форме:

lt = 0-

Сумма комплексных значений токов в любом узле цепи равна нулю.

Поскольку комплексные значения токов состоят нз действительных и мнимых частей, очевидно, должны быть равны нулю отдельно сумма действительных и сумма мнимых частей комплексных значений токов в узле цепи:

£/cosi/ = 0, Ersini} = a

Для любого замкнутого контура цепи переменного тока может быть-составлено уравнение мгновенных значений ЭДС, токов и напряжений по второму закону Кирхгофа: Zir + J.U.

Выразив ЭДС, токи и напряжения в комплексной форме, получим второй закон Кирхгофа в комплексной форме: