Далее определяют эквивалентные активное, реактивное и потное сопротивления параллельного участка цепи:

э-ээ; xbzl; z3-l/>v

В результате расчетов непь может быть заменена эквивалентной цепью (рис, 2.18,6), тде все сопротивления включены последовательно. Общие активное, реактивное и полное сопротивления цепн равны

Гоб = з + Лоб = х± .V

Цепь приобретает простейший вид, изображенный на рис. 2.18,в. Общий ток цепи определяют го закону Ома;

Напряжение между точками я и fc

= Iz, = f/y,.

Токи в параллельных ветвях равны

2.14. РЕЗОНАНС ТОКОВ

Резонанс токов может возникнуть в параллельной цепи {см. рис. 2.17, о), одна из ветвей которой содержит X и г, а другая Сиг.

Резонансом токов называется такое состояние цепи, когда общий ток совпадает по фазе с напряжением, реактивная мощность равна нулю и цепь потребляет только акгнвную мощность. На рис. 2.17, изображена векторная диаграмма цепи рис. 2.17,а при резонансе токов.

Как видно из векторной диаграммы, общий ток цепи совпадает по фазе с напряжением, если реактивные составляющие токов ветвей с индуктивностью и емкостью равны по модулю:

Общий реактивный ток цепи, равный разности реактивных токов ветвей, в этом случае равен нулю;

Общий ток цепи имеет только активную составляющую, равную сумме активных соошвляюших токов ветвей;

Выразив реактивные токн через напряжения и реактивные проводимосш, получим

откуда

Итак, при резонансе токов реактивная проводимос1Ь весви с индуктивностью равна реактивной проводимости ветви с емкостью.

Выразнв bi и bi через сопротивления соответствующей ветви, можно определить резонансную частоту контура:

2n/L

2-KjC 1

iKfC

InyLC

В идеальном случае, когда г

L/C - г]

2к\/Тс

При резонансе токов коэффициент мощности равен единице:

С05ф = 1.

Полная мощность равна активной мощности: S = P.

Реактивная мощность равна нулю: Q-Ql-Qc=0-

Энергетические процессы в цепи при резонансе гоков аналогичны процессам, происходящим при резонансе напряжений, которые были подробно рассмотрены в § 2.12.

Реактивная энергия действует внутри цепи: в одну часть периода энергия магнитного поля индуктивности переходит в энергию электрического поля емкости, в следующую часть периода энергия электрического поля емкости переходит в энергию магнитного поля индуктивности. Обмена реактив-

Pi5c. 2.19. Электрическая uciib (й и графики зависимости t It-. Ус и J от частоты f (6)

ной энергией между потребителями цепи и источником питания нс происходит. Ток в проводах, соединяющих цепь с источником, обусловлен только актив1юй мощностью

Для резонанса токов характерно, что общий юк при определенном сочетании параметров цепи может быть значительно меньше токон

а значение тока

в каждой встви. Например, в идеальной цепи, когда г, - г, = О (см. рис. 2.18, й). общий ток равен пулю, а токи ветвей с емкостью и индуктивностью существуют, они равны по модулю и сдвинуты по фазе на 180 . Резонанс в цепи при параллельном соединении потребителей называется резонансом iOKOB.

Резонанс токон может быть получен пзтем подбора пара--мегров цепи при задашюй частоте источника питания или путем подбора частоты источника питания при заданных нараме-ipax депи.

Представляет интерес влияние частоты исючнлка питания на значения токов в цепи, например в цепи, изображенной на рис. 2.19, д.

Ток в ветви с индуктивностью обратно пропорционален частоте:

U/2nfL,

а ток в нетви с емкостью прямо пропорционален частоте: Ic=V2TifC.

Ток в ветви с активным сопротивлением не зависит от частоты:

= и/г.

Век юр общего тока в цепн равен геометрической сумме векторов токов ветвей:

Если пренебречь s водника.

1иянием вытеснения тока к поверхности про-

При / = С

1= х:; /с =0; = и/г; I = do.

При/Д,

При / х

Графики зависимости 1 ч I от частоты изображены

на рис. 2.19, б.

Бопьгиинство промышленных потребителей переменного тока имеют акзивно-индукдивный характер; некоторые из них работают с низким коэффициентом мощносхи и, е.1едовазельно, потребляют значительную реак 1ивн)ю мощность. К таким потребителям относятся асинхронные двигатели, особенно работающие с неполной нагрузкой, установки электрической сварки, высовзчастотной эакал-

Для уменьшения реактивной мощности н повышения ухуэфтитентя. моицммгги параллельно потребителю включают батарею конденсаторов

Реактивная мощность конлснсаз оркой батареи уУ1еныггает общую реактивную мощность установки, так как

Q-Ql-Qc.

и тем самым увеличивает коэффициент мощности.

Повьппение коэффициента мощности приводит к уменьшению тока в проводах, соединяющих потребитель с исто-нгиком энергии, и полной мсящтости источпика.

Пример 2.5. Определить емкость конденсатора, прн которой в цепи рис. 2.20 возникает резоианс тсжов, если х, -40 Ом, г 30 Ом, Г2 = 28 Ом, / = 1000 Гц, I

Рис. 2.20. Электричестсая цепь к примеру 2.5 О

Решение. При реюнансе ( из нулю:

S мощность цеги рае

Oi-e, -U, н-та 61.= й,

г 40 =

30 + 40 28 + л-;- Емкость ксидснсаюра

о 7.75 Ом.

110*

2nfxc 2 3.14-1000-17,75

2.15. ПОНЯТИЕ О КРУГОВЫХ ДИАГРАММАХ

Иногда для анализа испей переменного чика целесообразно использовать Kpyi овые диаграммы.

Для любой электрической цепи може! быть изображена векторная диаграмма токов и напряжений.

Векторная диаграмма, в которой геомегрическое место точек конца вектора тока или наиряжения представляет собой дугу окружности при изменении napaMeipa какого-либо одного элеменга электрической цепн и неизменном напряжении, приложенном к цепи, называется круюиой диаграммой.

Рассмотрим векторную диаграмму простейшей электрической цепи (рис 221,0) и покажем, что она является круговой диаграммой. Уравнение напряжений цепи имес! вид U = + + Ll = J+ Xi.. Векторпаядиаграммаизображенл нарис 2.21,6. При измесюнии значения .\> одновременно изfeняютcя лна-чения тока, yuia ф и напряжений и U. но угол между векторами Or и остается неизменным и равным 90 , На рис 2.21,6 пунктиром изображена векторная диаграмма цепи для > xi , при этом

Ф>Ф, u;<Ur, Ui>Ui, /</.

Так как катеты прямоугольного треугольника напряжений (7, и Ul вменяются, а гипотенуза V остается неизмеппой, то вершина прямого >тла и. следовательно, конец вектора напря-

и и/г i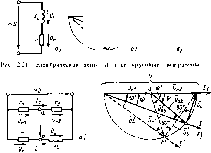

Рис. 2 12. Электрическая цепь {и) и ее круговая диаграмма (б)

жсния С\ будет описывать дугу окружности. Легко показать, что и коней вектора тока в этом случае будет описывать также дугу окружиостн. Действительно, если папряжегше U = 1г, а значение сопротивления резистора г остается неизмепным. то вектор тока / - V,/r будет описывать ду1у окружниаи, так же как и конец вектора напряжения 17, (рис. 2.21, в). При xiO Ф = 0, U/r; прн х> О 0<ф<90 ,

I = ... -------Ф -,-------------;

\/г + х Уг+х

прн Vi.= = 0- Ф=90 .

В системах автоматическою управлении находят применение фазоврашательные мосты, анализ и расчет которых удобно Производить с помощью круговых диа1рамм. Рассмотрим мостовую цепь, изображенную на рис. 2.22,0. и покажем, что при изменении одного из параметров цени, например значения сопротивления резистора г, при условии, что ri - Г;, напряжение между точками цепи а, b остается неизменным по модулю, но изменяется по фазе.

На рис. 2.22,0 изображена векторная диаграмма цепи рис. 2.22, U при двух значениях сопротивления резистора т <г.