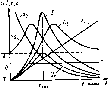Рис. 2.15. Графики зависимости 1, г. хс- [/ Vl, Ос от частоты цепи, изображенной на рис 2.11, д

циркулирует внутри контура и обратно. Обмена реактивной и цепью пе происходит. Ток источник с цепью, обусловлен

ковы, вся энергия Э1ектри-ческо! о поля конденсатора переходит в энергию магнитного поля индуктивности. Во вторую четверть периода, в интервале между точками 2 и 3, энергия магнитного поля переходит в энергию электрического поля.

Анало! ичные процессы происходят и в последующие четверти периода.

Таким образом, при резонансе реактивная энергия от индуктивности к емкости энергией между источниками в проводниках, соединяющих только активной мощностью.

Для анализа цепей иногда используют частотный метод, позволяющий выяснить зависимость параметров цени и других величин oi частоты.

На рис 2.15 изображены графики зависимости (/ 0, U[j, I. Хс, x[j от частоты при неизменном напряжении сети.

При / = О сопротивления \-=-2к/Ь = 0, Хс = У2я/Г= эз.ток / =0, напряжения L, = lr = 0, [/,.7x=0, Vc=V. При =/р,э х=хс, I-= и/г. Ul= Uc, и, - и. При/-, оох-. со. хс- 0, О ,-.О, UcO,

R интервале частот от/ = О до/ = fp нагрузка имеет акгивно-ем-костный характер, ток опережает по фазе напряжение сети. В интервале чаего! о / = fp до/-* oj Haip>jKa носи! ак1Иьно-инд>ктивный характер, ток отстает по фазе от напряжения сетн.

Наибольшее 1начение напряжения на емкости нолучаеин при частоте, несколько меньшей резонансной, на индуктивности - при частоте, несколько большей резонансной.

Явления резонанса широко используются в радиоэлектронных yciройс!вах и в заводских промышленных установках.

Пример 2.4. Определить частоту сети, при которой в цепи рис. 2.11,(1 возникает резонанс напряжений. Определить также, во сколько раз напряжение иа индуктивности больше напряжения сети при резонансе, если цепь имеет следующие параметры:

г = 20Ом, 1.= 0,1Гн, С = 5мкф.

Индуктивное сопротивление цепи при резонансе xl=2nfL-6ai22A-0,l = 1400м,

Напряжение на индуктивности при резонансе

Напряжение на индуктивности при резонансе в 7 раз больше напряжения сети.

2.13. РАЗВЕТВЛЕННЫЕ ЦЕПИ

Параллельное соединение прием1шков. Вначале рассмотрим i рафоаналитический метод расчета цепн с параллельным соединением потребителей (рис. 2.16,о). Для такой цепи характерно то, что напряжения на каждой ветви одинаковы, общий ток равен сумме токов ветвей.

Ток в каждой ветви определяется по закону Ома:

и и и

Vrl+xc

Vrl + {L,~Xc,f

Угол сдвига ф между током каждой ветви и напряжетшем о[1ределяют е помощью со5ф:

cos 9з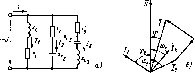

24/Zc 2-3,41,0,1510-

Рис, 2.16, Цепь с параллельным соедипенвем потребителей (а) ее векторная диаграмма (б)

Общий ток в цепи, как следует нз первого закона Кирхгофа, равен геометрической сумме токов всех ветвей:

Значение общею тока определяют графически по векторной диаграмме рис. 2.16,6.

Акшвная мощность цепн равна арифметической сумме активных мощностей всех .ветвей:

Реактивная мощность цепи равна алгебраической сумме реактивных мощностей всех ветвей: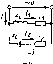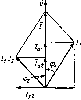

Рис. 2. п. Элек1риче€кая цепь (а), ее эекторнля диаграмма (б> и жйнна.тенгная с.чема {в; векторная дндграмма цени при рсэонансс

причем реактивную мощнос1Ь bcibh с индуктивностью берут со знаком плюс, ветви с емкостью - со знаком минус. Для цепи рис. 2.16 реактивная мощность равна

Q = QLi-Qcz + QLг-Qcъ.

Полная мощность цепн

S = ур 1 Q\

Угол сдвига ф между общим током и напряжением определяют из векторной диаграммы или из выражения: cos о - P/S.

1 рафоаналитический метод не удобен для расчета разветвленных цепей; он отличается громоздкостью и невысокой степенью точности.

Для анализа и расчета разветвленных цепей переменного тока используют проводимости, с помощью которых разнет-вле.чную цепь можно преобразовать в простейшую цеиь я аналитически рассчитать токн и напряжения всех ее участков.

В цепях постоянного тока проводимостью называется величина, обратная сонро1ивлению участка пепи:

и ток в цепи выражается как произведение напряасения на проводимость:

/ = Ug.

В цепях переменного тока существуют три проводимо-сги - полная, активная и реактивная, причем только полная проводимость является величиной, обратной полному сопрогн-влснию последовательного участка цепи.

Выражения нроводимостей в целях переменного тока можно получить следующим образом.

Так в каждом неразветв.тснном участке цепи раскладывают на дэе составляющие, одна hj коюры. ccib проекция на вектор напряжения [активная составляющая тока /J, а лругая - на линию, перпендикулярную вектору напряжения (реактивная составляющая тока /р).

Активная составляющая тока определяет активную мощность

Р= Uicosqi- и/а; реактийчяя составляющая тока - реактивную мощность

Из векторной диаграммы цепи рис. 2.17, а, июбраженной на рис. 2,17,6. следует, что активная составляющая тока равна и г

iij = I, созф, = -- = UrJz-\ = Ug.

называется активной проводимостью bcibh. Реактивная составляющая тока /, равна

называется реактивной проводимостью ветви цепи с индуктивностью н в обшем случае обозначается Ь[.

Аналогично определяют активную g-i и реактивную проводимости второй ветви цепи:

/2а - Ь COS - - rj/z, - Ug,; g, - r/2l /jp = i, sin фз = U/Zj-xc/z, = [/fcj; b, = ba = ЫА-

Реактивная проводимость встви с емкостью в общем случае обозначается Ье-

Вектор тока первой встви равен геометрической сумме векторов актииной и реактивной спставляюпих тока

4-Лр,

а значение тока

Выразив составляющие тока через напряжение и проводимости, получим

где у, = l/г = V+Wi - полная проводимость ветви.

Аналогично определяют и полную проводимость второй ветви:

Уг = = VgUC-

Эквивалентные активную, реактивную и полную проводимости цени получают следующим образом.

Вектор общего тока цепи равен геометрической сумме векторов

токов i II

i=h +h

и может быть выражен через активную и реактивную составляюшие тока и эквивалентные проводимости всей цепи:

/ + ip Ug, +йЬ = Uy = [ z,.

Активная составляющая общего тока (см. рис. 2.17,6) равна арифметической сумме активных составляющих токов ветвей;

h-f, + hB Vg, + Vg= Uigi +g2)=Vg (2.24)

a реактивная составляющая - арифметической разности реактивных составляющих этих токов:

fp - P tL, - Ubc, = C(bi., - fee.) = иЬ,. (2 25)

Рис. 2.18, К расчету разветвленной цени с использованием про лпмпстей

Из выражений (2.24) и (2.25) следует, что эквивалентная активная проводимость цепи равна арифметической сумме активных проноди-чгостей параллельно включенных ветвей:

?э-Й1 +gi+ (2-26)

а эквивалентная реактивная проводимость - алгебраической сумме реактивных проводимостей параллелыю включенных ветвей:

h=bn-\-bc2+ + Ь[.п + Ьсп. {2.21)

При этом проводимости ветвей с индуктивным характером нагрузки берут со знаком плюс, ветвей с емкостным характером нагрузки - со знаком минус.

Полная эквиваленшая проводимость цепи

У. = h% = ]/g + Ь1 (2.28)

По эквивалентным активной, реактивной и полной проводимо-стям можно определить параметры эквивалентной схемы (рис. 2.17, в) цепи.

Эквивалентные активное, реактивное и полное сопротивления цепи определяют с помощью выражений

г. = r,-gl x, = b,zl

Необходимо отметить, что если Y.LY.c эквивалентное сопротивление х., будет индуктивным, если X с > Z ь емкостным.

Смешанное соединение потребителей. Расчет цепи при смснзанном соединении потребителей (рис. 2.18,о) может быть произведен путем замены ее простейщей эквивалентной цепью. Для этого вначале определяют активные, реактивные и полные проводимости параллельно включенных ветвей: i, g, b bj. у v,.

Затем находят эквивалентные активную, реактивную и полную проводимости параллельного участка пени: