Инлуктинность /- определяют из формулы

Пример 2.1. Приборы, включенные в цепь рнс 2.13, ncKaibi-ляк,т- Р - 500 Вт, / = 5 А, (J = 400 В.

Оирслелить активное сопротивление г и индуктивность иепи L, если частота сети / = 5ЙГц.

Решение. Активное соиротв.и-ние цетти

г = Р = 500/5 = :ООы. ,1,роиш1ение цепи

Индукти!

= \/ = /(U )--r = 1/(400/;) - 20 - 77,5 Ом. Индуктивность пени

Т7 Ч

= 0,247 Ги.

2т;/ 2-3,14.50

Пример 2.2. Определить ток, полную, активную и реактивную мощности, а также налряж-ения на отдельных участках цепи, изображенной на рж.. 2 11,и. если г = 40Ом. L=0,382rH, С = 15,5мкФ, 11 гг 220В, частота сети / = 50Гц,

Решение. Индуктивное сопротивление цени

.>i,= 27[/L=2-3,14-500,3S2= 120Ом. Емкостное сопротивление цени

= 90 Ом

27u/C 2-3,14.50.35,5

Полное сопротивленне пепи

7 = \{<iXcY - /4\) + i 12У - -JO? = 50Ом

i - - 220/50 = 4.4 А.

Коэффициент

cos ф = г/2 = 40/50 = 0,8.

Потная, авт1-!вная п реактивная моииюспи:

S= (.7 = ;=- 220 4,4 = -1,4--50 -970 В-А.

Р = Scm ф = /-г 970 0,8 = 4,4 40 = 775 Вт; е = Ssin ф = (.v- Хс) - 970-0,56 = 4.4(120 - 90) - 580вар. Напряжения на oijcjibiibix участках цели: V, = /г =4.4-40 = ]76 В, V:-1x4.4 120 = 52Ка; Vc = lxc-4,A 90 = 196 В.

Пример 2.3. Определить характер нагр>-1ки, полную, aKiHBfiyio и реактивную мошностн неги, в которой м[ ноаенные значения напряжения и тока состав 1яют

* = 2l2sin [<at + 601.

1 - 141 sin {at + Ш).

Решение. Угол начальной фазы напряжения (tf, =60 ) бо 1ьше, le.M тока (((j = 30-), поэтому напряжение опережае: ли фазе ток на угол ф - - ф, = 60 - 30 = 30 и HaipyTO имеет активно-индуктивный характер

Полная мощность цеп

S=U] = -

282-14]

= 20 ООО В - А.

/2 /2 ],4М,41 Активная мощность иепи

Р = 5созф = 20 ООО ens 30- = 20 ООО (I/3/2) - 17 300 Вт Реактивная мощность цепн

е-5з1пф = 2O00Oiin30 = 20000-0,5- 10000 вар.

2.U. ЗАКОНЫ КИРХГОФА В ВЕКТОРНОЙ ФОРМЕ

Анализ и pac4ei сложных цепей переменного тока, так же как 1г цепей постоянного тока, производятся с помощью уравнений электрического состояния, составленных го законам Кирхгофа. Для цепей переменного юка во многих случаях це-.1есообразнее записывать уравнения электрического состояния цепей по законам Кирхгофа в векторной фирме. На основании уравнений, записаппьпс в векторной форме, легко построить векторную диаграмму.

Согласно первому закону Кирхгофа сумма токов в у1ле равна нулю при любом законе изменения токов во аремени Si-O. Для замкнутого контура электрической цспп может быть записано уравнение по второму закону Knpxi офа, связы-

пающее мгновенные значения ЭДС, токов и напряжений независимо от того, по какому закону изменяются эти величины:

1е = Sif + Su.

В цепях синусоидальных ЭДС ток и напряжение изменяются синусоидально, поэтому они могут быть нредсхавлены вращающимися векторами и законы Кирхгофа записаны в векторной форме-

Переый закон: Геоме1рическая сумма токов узла равна нулю:

Е/= 0.

Второй закон: Геометрическая сумма ЭДС при обходе но saMKHjTOMy контуру равна геометрической сумме произведений токов на полные сопротивления соотвгтствутпих ветвей контура плюс геометрическая сумма напряжений, действующих в контуре:

Знаки перед соответствующими членами уравнения определяются так же, как и для цепей постоянного тока: при совпадении направлений Е, I, U z паправлепием обхода контура перед соответствующим uieiiuM уравнения проставляется знак плюс, при несовпадении - знак минус.

2.12. РЕЗОНАНС НАПРЯЖЕНИЙ

Известно, что в механической системе резонанс накупает при равенстве собственной частоты колебаний системы и частоты колебаний возмущающей силы, действующей на систему. Колебании механической системы, например колебания маятника, сопровождаются периодическим переходом кинетической энергии в потенциальную и наоборот. При резонансе механической системы малые возмущающие силы могут вызывать большие колебания системы, например большую амплитуду колебаний маятника.

В цепях переменного тока, где есть индуктивность и емкость, могут возникнуть явления резонанса, которые аналогичны явлению резонанса в механической сисеме. Однако полная аналогия - равенство собственной частоты колебаний электрического контура частоте возмущаюп1ей силы (частоте напряжения сети) - возможна не во всех случаях.

В общем случае иод резонансом электрической цепи пони-

мают такое сосюяние пепи, когда ток и напряжение совпадают по фазе, и, следовательно, эквива-тентная схема цепн представляет собой активное сопротив.1ение. Такое состояние цепи имеет место при определенном соотношении ее параметров г. L. С, когда резонансная частота цепи равна часдоте приложенного к ней напряжения.

Реюнанс в электрической цепи сопровождается периодическим переходом энергии электрического поля емкости в энер-1ИЮ магнитного поля индуктивное!и и наоборот.

При резонансе в электрической цепи малые напряжения, приложенные к цепи, могут вызвать значительные токи и напряжения на отдельных ее участках В цени, где г, L, С соединены последовательно, может возникнуть резонанс напряжений, а в цепи, где у, L, С соединены параллелыю.- резонанс .токов,

Рассмотри.м явление резонанса напряжений на примере цепи рис. 2 11,0.

Как отмечалось, прн резонансе ток и напряжение совпадают по фазе, т. е. угол ср = О, и полное сопротивление цепи равно ее активному сопротивлению.

Эю равенстБО, очевидно, буде! иметь место, есди у, = дг, т. е. ргакгивное сонротивленне пепи равно нулю:

x Xi-.Xc = 0.

Выразив и хс соотзетствеипо через L, С н /, получим 1

2n/L =

InfC

2пу1ё

где f - частота напряжения, подведенного к контуру; /рез - резонансная частота.

Таким образом, при х-с пени возникает резонанс напряжений, так как резонансная частота равна частоте напряжения, подведенного к цепи.

Из выражения закона Ома для последовательной цепи V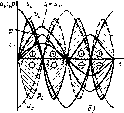

Рис. 2,14. Векторная диаграмма (a) и графики мгновенных и, I, р (б) цепи рис. 2.11. а при резонансе напряжений

вытекает, что ток в цепи при резонансе равен напряжению, деленному на активное сопротивление: I = и/г.

Ток в цепи может оказаться значительно больше гока, который был бы при отсутствии резонанса.

При резонансе напряжение иа индуктивности равно напряжению на емкости:

[X, = Ixr =и, и г.

При больших значениях .Vl и Хс относительно г эти напряжения могут во много раз превышать напряжение сети. Резонанс 3 цепи при последовательном соединении потребителей НОСИ1 нашание резонанса напряжений.

Напряжение па активном сопротивлении при резонансе равно напряжению, лриЛ1)женному к цепи: U=Ir=V.

На рнс. 2.14,а изображена векторная диаграмма цепи рис. 2,и,я при резонансе напряжений

Диаграмма подтверждает тот факт, что ток совпадает по фазе с напряжением сети и что напряжение на активном сопротивлении равно напряжению сети.

Реактивная мощность прн резонансе ранна нулю:

так как Ul= Uc-92

Полная мощность равна активной мощности: S = ур + Q = P,

так как реактивная мощность равна нулю. Коэффициент мощности равен единице:

С05ф = f/S = r/j= ].

Поскольку резонанс напряжений возникает, когда индуктивное сопротивление последовательной цепи равно емкостному, а их значения определяются соответственно индуктивностью, емкостью цепн и частотой сети.

Резонанс может бы]ь получен или путем подбора параметров цепн при заданной частоте сетн, нли путем подбора частоты сети нри заданных параметрах цепи.

На рис. 2.14,р изображены графики мгновенных значений тока 1, напряжения и сети и напряжений ь и, на отдельных участках, а также активной р = iu, и реактивной pl= рс = шс мощностей за период для цепн рис, 2,11, й прн резонансе напряжений. С помощью этих графиков можно цpocJ[eдить чнергети-ческне процессы, происходящие в цепи прн резонансе напряжений.

Активная мощность р все время положительна, она поступает из сети к активному сопрошалению и выделяется в нем в виде тепла. Мощности н рс знакопеременные, и, как видно из графика, нх средние 1начения равны нулю.

В момент времени г = 0 (точка / на рис. 2.14,(5) ток в пени ( = 0 и энертя магнитного поля - О. Напряжение на емкости равно амплитудному значению и с, конденсатор заряжен и энергия его электрического поля

В первую четверть периода, в интервале времени между точками J н 2, напряжение на емкости н, следовательно, энергия электрического поля убывают. Ток в пепи и энер1ия Mai-нитного поля возрастают.

В конце первой четверти периода (точка ?) uc = О, Wc-0.

Таким обрачом, в первую четверть периода энергия электрического поля переходит в энергию магнитного поля.

Так как площади pc{t) и pj (r), выражающие запас энергии соответственно в электрическом и магнитном полях, одина-