2.6. ЦЕПЬ. СОДЕРЖАЩАЯ ЕМКОСТНЫЙ ЭЛЕМЕНТ С ЕМКОСТЬЮ С

В радиоэлектронных устройствах емкость является элементом колебательных контуров, фильтров, элементом связи между контурами и т. п. В силовых установках конденсаторы используют для улучшения коэффициента мощности, как элемент колебательного контура высокочастотных установок для закалки и плавки металлов. В любой электрической уста1ювке емкости образуются между проводами, проводами и землей и другими элементами токоведущих конструкций.

При большой протяженности проводов емкость может оказаться значительной, и при расчете цепей даже низкой, например промышленной, частоты ее необходимо учитывать. В высокочастотных цепях даже небольшие емкости оказывают существенное влияние на режим работы цепи и их необходимо учитывать.

Ток в цепи с емкостью (рнс. 2.8, а) представляет собой движение зарядов к ее обкладкам:

i = dq/dt. (2.10)

Выразив в (2.10) заряд q через емкость С и напряжение на емкости Не, из выражения

C=q/uc

получим

I- Cduc/dt.

Напряжение на емкости изменяется синусоидально:

u = Uc= и sin (Of. (2.11)

Тогда ток в цепи

i=C-

dV , sin Mf

Взяв производную, Получим мгновенное значение тока в цепи с емкостью:

(2.12)

I = (oCl/cos(o( = sin ((Of -f KJl).

Сравнивая выражения (2.11) и (2.12), можно сделать вывод, что ток в емкости опережает напряжение на емкости по фазе иа 90 .

Векторная диаграмма цепи с емкостью приведена на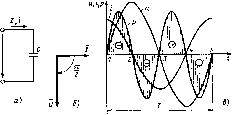

Рис. 2.8. Электрическая цепь, содержащая емкостный элемент с емкостью С (а), ее векторная диаграмма (б) и графики мпювенных значений и, i, р (в)

рис. 2.8, 6, а график мгновенных значений тока н напряжения -на рис. 2.8, е.

Напряжение и ток в цепи с емкостью, как следует из выражения (2.12), связаны соотношением

= соС(7 ,

откуда

= (2.13)

1/(оС

Разделив левую и правую части (2.13) на yl, получим закон Ома для цепи с емкостью:

1/(оС хс

(2.14)

где Хс = 1/ * ~ емкостное сопротивление. Ом.

Таким образом, иапряжение на емкости в цепи переменного тока может быть выражено через произведение тока на емкостное сопротивление:

и =Vc = Ixc.

Мгновенное значение мощности р в цепи с емкостью равно произведению мгновенных значений напряжения и тока:

p = ui= sin (of/ sin (tot + %/2) = f sin 2(of = Vl sin l(ut =

= P sin 2(of.

Из полученного выражения вытекает, что мгновенная мощность изменяется по закону синуса с частотой, в 2 раза большей частоты тока, и ее амплитудное значение

Р = UI.

Среднее значение мощности за период (активная мощность), как видно из графика рнс. 2.8,6, равно нулю: т

Р = -

uidt = 0.

Для пояснения энергетических процессов в цепях с емкостью воспользуемся графиками, изображенными на рис. 2.8, е. В первую четверть периода, в интервале времени между точками I и 2, напряжение на конденсаторе возрастает, происходит заряд конденсатора: электрическая энергия из сети поступает к конденсатору и накапливается в нем в виде энергии электрического поля. Накопленная энергия равна заштрихованной площади, ограниченной кривой р(() (отмечена знаком + ), и составляет

т/4 Г/4

ui dt =

sin 2ш dc

В следующую четверть периода, в интервале времени между точками 2 и 3, ток изменяет направление, а напряжение на конденсаторе убывает. Происходит разряд конденсатора: энергия электрического поля возвращается в сеть. Энергия, возвращенная в сеть, равна- площади, ограниченной кривой p{t) (отмечена знаком - ).

Из графиков рис. 2.8, в видно, что плошади, определяющие запасенную и отданную энергии, равны. Следовательно, энергия, накопленная в электрическом поле емкости в первую четверть периода, полностью возвращается в сеть во Вторую четверть периода.

В следующую четверть периода, в интервале времени между точками 3 и < изменяется полярность напряжения на обкладках конденсатора. Происходит заряд конденсатора: электрическая энергия из сети поступает к конденсатору и накапливается в нем в виде энергии электрического поля. В последнюю четверть периода, в интервале между точками 4 я 5, происходит разряд конденсатора: энергия электрического поля возвращается в сеть.

Таким образом, в цепн с емкостью, так же как и в цепи с индуктивностью, происходит непрерывный периодический процесс обмена энергией между сетью и конденсатором.

2.7. ЦЕПЬ, СОДЕРЖАЩАЯ КАТУШКУ С АКТИВНЫМ СОПРОТИВЛЕНИЕМ г И ИНДУКТИВНОСТЬЮ L

Реальная катушка (обмотка) любого электротехнического устройства обладает определенным активным сопротивлением ) и индуктивностью L. Для удобства анализа таких цепей катушку обычно изображают в виде двух идеальных элементов - резистивного г и индуктивного L, соединенных последовательно (рис. 2.9, а). Используя выводы, вытекающие из анализа идеальных цепей, участок цепи с индуктивностью L будем рассматривать как участок, обладающий индуктивньпи сопротивлением хи Уравнение напряжений, составленное по второму закону Кирхгофа для цепи с г и L, имеет вид

и = н, -t- tJi.-

Выразив напряжения и н, через ток i - 1 sin at и сопротивления участков цепи г и х, получим

и = 1 г sin eat + ixsin I wf --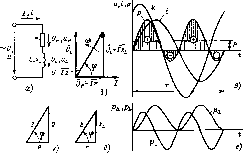

Рис. 2.9. Электрическая цепь, содержащая катушку индуктивности г и L (а), ее векторная диаграмма (б), графики мгновенных значений и, /, р (в), треугольники мошностей и сопротивлений (г, д), графики мгновенных значений р, р£, (е)

где ((, = Irdnm - напряжение на am ивном соиро[MHJieHkH (активное напряжениеХ совпадающее по фазе с током; (( = = / ,xj,sin (iiw + тг/2) - напряжение на индуктивном сопротивлении (индуктивное напряжение), опережаю[1ее юк по фа1е на 90 .

На векторной диаграмме (рис. 2.9,6) вектор 0 совпадает с вектором тока, а вектор (}( опережает вектор тока на 90-.

Из диаграммы следует, что векюр напряжения се1и ранен геометрической сумме векторов О, и О.

и и,+ L7l,

а его значение

Выразив напряжения через ток и сопротивления, [[OjiynnM Последнее выражение представляет собой закон Ома пепи г.

1 = -

где Z = [/+ Х] - полное со[]ро1ивление цепи. Ом.

Из векторной диаграммы следует, что напряжение цепи г, Loiiepe aei чо фазе ток на угол ф и его мгновенное значение

и = 1) sin (га/ -I- <р)

Графики мгновенных значений напряжения в тока цепи изображены на рис. 2.9, е.

Угол сдвига по фазе ф между напряжением в вызванным им током определяют из соотношения

V, Jr г г

cos ю = -- = - = - = - ---

(2.15)

Как видно, cos ф и, следовательно, угол ф зависят только от нарамефов цепи г и Xi.

Разделив стороны треугольника напряжений на ток, noiy-чим треугольник сопротивлений (рис. 2.9, d), Стороны треугольника сопротивлений представляют собой отрезки, а не векторы,

так как сопротивления есть постоянные, не изменяющиеся синусоидально величины.

Мгновенная мощность цепи с г и L равна произведению мгновенных значений напряжения и тока:

р = ui = sin car sin (or + ф). Средняя мощность за период

1 и, sin ш sin (tor + ф) dt.

Выразив произведение синусов через разность косинусов, после почленного интегрирования получим

-[созф - cos(2a)f -j- ф)] dt = UJcos ф. (2.16)

ПодС1инив в (2.161 вместо шя ф ею значение из (2.15), получим

- I cos ф - (71 - - J V Р.

(2.17)

И* (2.17) вытекает, что сре;1нее значение .mueuhocih в цени С J и L есть активная мощность, которая вьшеляется в актив-пом сопротивлении г в виде теплоты.

График мгновенной мощности изображен на рис. 2.9, е.

Длн анализа знер[ ei ических пронессоя в цепи г, L мгновенную мощность удобно представить в виде суммы мгновенных значений активной pa = i и реактивной (индуктивной) pL= И[! мощностей:

РР + Рь

Графики Ра it), p, (t) изображены на рис. 2.9, е. График pt} гшалотичен графику дтя цепи с активным сопротивлением (см. § 2,4), а график р(, (t) - для цепи с индуктивностью L (см. 2.5).

Таким образом, энергетические процессы в цепи с г, L можно рассматривать как совокупность процессов, происходянщх в цепях только с активным сопротивлением г и только с индуктивностью L.

Из графика р (г) видно, что активная мощность непрерывно поступает из сети и вьщеляется в активном сопротивлении