2.4. ЦЕПЬ, СОДЕРЖАЩАЯ РЕЗИСТИВНЫЙ ЭЛЕМЕНТ С АКТИВНЫМ СОПРОТИВЛЕНИЕМ г

В общем случае электрическая цепь переменного тока может содержать резистивные, индуктивные и емкостные элементы, параметрами которых соответственно являются сопротивление г, индуктивность L н емкость С. Анализ и расчет таких цепей значительно сложней, чем цепей постоянного тока. В цепях постоянного тока индуктивные и емкостные элементы проявляют себя только в моменты включения, отключения цепи или изменения ее параметров, когда изменяется юк и ио-является ЭДС самсжндуктщи е = Ldi/dt в индуктивном элементе

и напряжение uc = -на емкое том элементе.

В установившемся режиме ток в цепях постоянного тока не изменяется и ЭДС самоиндукции равна нулю, а напряжение на емкости uc соотвегствус! какому-то постоянному значению.

В цепях переменного тока происходит непрерывное изменение напряжения н.тока, в результате чего возникает изменяю-шаяся во времени ЭДС самоиндукции е в напряжение на емкости Uc.

Таким образом, режим работы цепи перемегиюго тока определяется не только сопротивлением г, но индуктивностью L и емкостью С. Прежде чем разбирать общий случай цепн с г. La С, остановимся на частных случаях.

Рассмотр1Ш цепь, содержащую только рсзистивный злемснт с активным сопротивлением г. Под ак1ивным сопротивлением понимают иопротивлепие проводников переменному току. Вследствие вытеснения тока к ооверхпостн проводника сопротивление проводника переменному току больше, чем постоянному. При малых частотах (несколько десятков и сотен герц) увеличение сопрогивления незначительно н активное сопротивление Определяется по той же формуле, что - н сопротивление постоянному току. При частотах в coihh тысяч и миллионы терц акзивное сопротивление может оказаться намного больше сопротивления постоянному току и для его определения используют соответствующие формулы.

Мгновенное значение тока в цепи с активным сопротивлением (рис 2.6,а) определяется по закону Ома:

Выразив и через амплитудное значение u=Usmtot,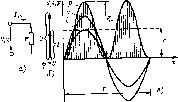

Рис 2-6. Электрическая цепь, содержащая рсзис-гавщ,1Й элемент с активным сичротиалсыием г (а), сс векторная диаграмма (о ) и графики мгновенных значений к, г, р (в)

получи

= 1 sin (ut,

(2.3)

L - и Jr.

Разделив левую и правую части на [/2, получим закон Ома лля цепи с активным сопротивлением, выраженный через действующие значения напряжет! и юка.

I = и/г.

Из выражения (2.3) следует, что ток и напряжение совпадают по фазе. Векторная диаграмма цепи изображена иа рис. 2.6,6. а график мгновенных значений тока и напряжения - на рис. 2.6, д.

Мгновенная мощность цепи равна произведению мгновенных зиачсни!! напряжения и тока:

pui и sina) sin <ot.

Из графика мпювениой мощности (рис. 2.6,в) видно, чю мощнос1ь изменяется от нуля до Р , оставаясь все время положительной. Это означает, что в цепи с активным сопротивлением энергия все время поступает из сети к приемнику г и необратимо преобразуется в нем в теплоту, которая нагревает сопротивление и рассеивается в окружающей среде.

среднее значение мощности за период

UJ 1-со8 2ш( UJ

Выразив амплитудные значения напряжения и тока через действующие значения, пачучнм

После подстановки U 1г будем иметь

(2.4)

Из выражения (2.4) вытекает, что феднее значение мощности есть электрическая мощность, которая преобразуется в активном сопротивлении в теплоту. Такую мощность называют активной и обозначают символом Р.

К приемникам активной мощности относятся также электрические двигатели, в которых электрическая мощность преобразуется в механическую мощность, развиваемую двигателем иа валу.

Активная мощность измеряется ваттметром, включенным соответствующим образом в электрическую цепь переменного тока.

2.5. ЦЕПЬ, СОДЕРЖАЩАЯ ИНДУКТИВНЫЙ ЭЛЕМЕНТ С ИНДУКТИВНОСТЬЮ L

Обмотки (катутики) электрических машин, трансформаторов, магнитных усилителей, электромагнитов, реле, кон1акто-ров, индукторов электрических нагревательных устройств и печей переменного тока обладают значительной индуктивностью. В радиотехнических устройствах индуктивные катушки используются для образования колебательных контуров, электрических фильтров и т. п. Параметрами катушек являются активное сопротивление г и индуктивность L. Изменяющийся во времени ток наводит в этих катушках ЭДС самоиндукции, которая по значению во многих случаях заметно больше, чем падение па-пряжения на активных сопротивлениях.

Рассмотрим вначале катушку, активное сопротивление которой настолько мало, что им можно пренебречь.

Для выяснения процессов, происходящих в цепи с индуктивностью (рис. 2.7, о), допустим, что ток в иидуктнвностн изменяется синусоидально

i = sm Ш. (2.5)

-и, и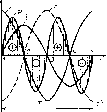

Рис. 2.7. Электрическая цепь, содержащая индуктивный элемент с индуктивностью L (а), ее векторная диаграмма (й) и графики мгновенных значений и. i, р (в)

Ток вызывает в индуктивности ЭДС самоиндукции

i.- -Ldi/dt. (2.6)

Уравнение, составленное по второму закону Кирхгофа для данной цепи, имеет вид

eL= -и. (2.7)

Выразив et и i через их значения нз (2.5) и (2.6). найдем напряжение на индуК1Ивности:

dl sin (Of

u = L-

Выполнив операдию дифференцирования, получим и = (oUcosoH = (oUsin I (Of -ь ~\ = U&ixiUut + у \ (2-8)

Из сравнения выражений (2.5) и (2.8) можно сделать вывод, что ток в цепи с индуктивностью и напряжение на индуктивности изменяются по синусоиде, а напряжение опережает по фазе ток на угол 90 .

Векторная диаграмма цепи с индуктивностью изображена на рис. 2.7,6, а графики мгновенных значений тока и напряжения - па рнс. 2.7, о.

Напряжение и ток в цепи с индуктивностью, как следует из

выражения (2.8), связаны соотношением

J = V /ii>L (2.9)

Разделив левую и правую час1и (2.9) на /2, получим закон Ома для цепи переменного тока с индуктивностью.

где XL=:a)L = 2ti:/L-индуктивное сопротивление, Ом.

Представив в (2,7) ЭДС самоиндукции и напряжение векторами, получим уравнение цепи в векторной форме для дей-сжуккцих значений

Е-и.

илн после замены наиряжения произведением тока и индуктив-пого сопротивления

Таким образом, ЭДС самоиндукции может быть выражена через ток и индуктивное сопротивление. Такой способ выражения ЭДС во MHuiHx случаях значительно упрощает анализ цепей с индуктивностью.

Мгновенная мощность цепи с индуктивностью равна

p = ui = 1 sin 0)1 и sin а)( + - sii

= Р sin 2ш.

sin 2(01 = UI sin 2(01 =

Мгновенное значение мощности (рис. 2.7, в) изменяется синусоидально с частотой, в 2 раза большей частоты тока. Амплитудное значение мощности

Р = Ui-

Легко показать аналитически и вз графика рис. 2.7, в, что среднее значение мощности за период (активная мощность) равно нулю:

P = yjui(fl = 0.

Для пояснения энергетических процессов в цепи с индуктивностью используем график рис. 2.7, е.

В интервале времени от t = О (точка J) до г = Г/4 (точка 2), когда 1 ок в цепи возрастает от О до / . электрическая энергия из сети поступает в индуктивность, преобразуется и накапливается в ней в виде )нергии магнитного поля.

Наибольшее значение энергии магнитного поля булег в mombhi времени, соответствующий точке 2, когда ток достигает амплитудного

Можно показать, что эта энергия равна заштрихованной гиющади графика р = /(() в интервале времени между точками i и 2 (отмечена знаком + >, Действительно,

Wi= \ ui dt= Z sin 2Ш 4t У I -cos2ojJ * = - -

III 1

В ин[ервале времени между точкшйн 2 и 3 ток в цепи убывает. Энергия магнитного поля преобразуется в электрическую энергию и возвращается в есть. В момент времени, соответствующий точке 2, ток и энергия магнитного ноля равны нулю.

Энергия, отданная в сеть, равна заштрихованной площади графика р = /(() в интервале времени между точками 2 и 5 (отмечена знаком < - ), Из графиков рис. 2.7, в видно, что площади, определяющие запасенную и отданную энергию, равны. Следовательно, энергня, накопленная в магнитном Ho.ie индуктивности в первую четверть периода, полностью возвращается в сеть во вторую четверть периода.

В следующую четверть периода в интервале времени между точками J н 4 изменяются направления тока и ма! ни того потока. Происходит процесс, аналогичный процессу в первую четверть периода: энер-1ия из сети [lociynacT в индуктивность и накапливается в ней в виде энергии магнитного поля. В последнюю четверть периода в интервале времени между точками 4 и 5 энергия магнитного поля возвращается в сжть.

Таким образом, в цепи с индуктивностью происходит непрерывный периодический процесс обмена энергией между сетью (источником энергии) и индуктивностью.