мость учета микроскопических свойств воды и ее растворов, ее аномальных реологических, электрических и других свойств в объеме и в области межфазных границ.

В этом разделе основное внимание уделено природе микроскопических и микрогидродинамических явлений, возникающих в водных средах в электрических и магнитных полях.

Явления, рассматриваемые в работе, затрагивают лишь частотный диапазон, в котором имеет место явление текучести жидкости, исчезающее при более кратковременных воздействиях внешних сил, т. е. диапазон времени действующих магнитогидроди-намических и электрогидродинамических давлений ограничен условием AtU, где 0 - время трансляционного перехода иона. Это время составляет для тонких слоев толщиной 6 0,1 мм 10-- 10~ с, а в объеме - значительно меньшие значения. Отметим-, что для молекулы воды to имеет тот же порядок.

При отсутствии внешних сил движение иона происходит беспорядочно: ион постепенно перемещается, совершая колебания около каждого положения равновесия. Скорость иона во время трансляционного перехода и при движении около положений равновесия при обычных температурах определяется средней скоростью теплового движения Утл/кТ/гпг, где й -постоянная Больцмана, гпг - масса иона [135].

Оценим величину Vt. Так как й=1,381 lO-* Дж!/К, то, приняв 7=300 К, mi= 10-2 кг, получим Ут=200 м/с. Причем для ионов ОН , Н+, или, точнее, НзО+, где m, меньше, Vt - значительно выше. Общее число таких переходов для ионов [124]

J = Joexp(-WolkT), (1.1)

где Wo - энергия активации.

Рассмотрим водный раствор сильного бинарного одновалентного электролита ао=1, (оо - коэффициент диссоциации). Раствор будем считать бесконечно разбавленным, т. е. не будем учитывать взаимного влияния ионов. Примем, что в растворе созданы стационарные взаимно перпендикулярные электрические и магнитные поля (Е±Н), градиенты которых равны нулю (VE=0, V Н = 0).

Представим рассматриваемую жидкость, как это обычно делают, в виде простейшей модели - твердых невзаимодействующих шариков, число которых 2Lco, где L - число Авогадро, Со - концентрация в грамм-эквивалентах. Будем учитывать только тепловое движение ионов, так как непосредственное влияние магнитного поля на молекулы решетки воды будет мало из-за теплового характера движения. Трансляционное движение ионов будет носить тот же характер, что и тепловое движение молекул воды, т. е. время нахождения иона около квазиравновесного состояния

fp = 0,5 ехр (ttJo/йГ). (1.2)

При наложении на подобную систему однородного постоянного магнитного поля (уЯ=0) энергия взаимодействия поля с ионом [аб Я<йТ, где ЦБ -магнетон Бора, Я -напряженность магнитного поля.

в случае когда сила, действующая на частицу, направлена перпендикулярно к скорости ее движения, она не совершает работы и не влияет на энергию частицы, лишь изменяя направление ее движения.

Так как энергия взаимодействия магнитного поля с ионом очень мала, то влияние магнитного поля не скажется ни на энер гии активации, ни на состоянии иона в положении равновесия. Это обусловливает то, что в момент перескока можно считать частицу относительно свободной и применять методы расчета, используемые для движения частиц в вакууме. Под действием силы

Рис. 1.1. Изменение траектории движения иона под действием магнитного поля.

/ - ион с зарядом ze\ 2 - новое положение иона после трансляционного перехода на расстояние 6 со скоростью Vj.; в - угол отклонения скорости иона Vj. от начального положения под действием напряженности магнитного поля И; г - радиус отклонения траектории иона при Н:0.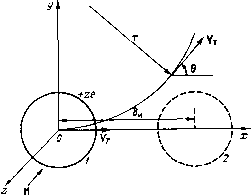

Лоренца 1л будет иметь место изменение траектории иона. В рационализованной форме

!л = Цо2е[УгХН]. (1.3)

где Z - зарядность иона; е - заряд электрона; цо - абсолютная магнитная проницаемость среды.

Учитывая современное состояние теории водных растворов, трудно определить, в какой именно момент происходит изменение импульса иона, однако можно все же отметить следующее. Полагая, что изменение импульса происходит только во время перехода, и используя основные представления о движении ионов в вакууме, изменение траектории иона можно представить следующим образом (рис. 1.1). Ион, имеющий заряд q = ze, совершает трансляционный переход на расстояние 6и, где би -расстояние между центрами 12 положений иона. Примем, что начало координат в центре иона в положении /, начальная скорость Уг = - Vx, H±V и при =0 Уг = соп51. Для иона в вакууме при Н=70 вектор скорости иона отклоняется на угол 6. Расчет [51] показывает, что этот угол на столь малом пути направления движения иона существенно не меняется. Более вероятным представляется существенное изменение импульса в начальный момент трансляционного перехода. Скорость ионов в этот момент не остается

равной Vt, а может быть значительно больше, так как ион обладает дополнительной энергией и во время перехода происходит рассеяние энергии за счет взаимодействия с окружающими молекулами воды. Следует ожидать, что величина !л по (1.3) будет максимальной в начальный момент, особенно приУтХН. Более строгое решение возможно лишь при учете локальных эффективных электрических полей, составляющих порядка 106 в/см.

Полагая, что изменение импульса иона под действием магнитного поля реализуется за время о, получаем

Дрш--=Рог е[УшХН]/о, (1.4)

где Zih - зарядность иона; i - сорт иона; k - число ионов t-того сорта, k - принимает значения от 1 до ; / - принимает значение 1 - /, а / - число перескоков в единицу времени.

При данном рассмотрении мы не учитывали явно роль ионной атмосферы. Этот эффект фактически выражается в создании в области нахождения иона локального флюктуационного электрического поля. Однако количественное влияние этого поля даже на такой важнейший показатель, как электрическая проводимость, относительно мало.

Особый интерес представляет действие магнитного поля на ионы гидроксония НзО+, которые, по-видимому, в какой-то момент времени существуют в виде свободного протона, а также на

отрицательный ион eeg (гидратированный электрон) [137].

Расчет макроскопической скорости потока. Рассмотрим водный раствор нескольких сильных электролитов. Примем, что вещества полностью диссоциированы, и коэффициент диссоциации равен единице. Концентрацию раствора примем достаточно малой, что позволяет пренебречь электростатическим взаимодействием ионов. Пусть Lci - число ионов t-Toro сорта, d - концентрация i-того иона.

Течение вязкой жидкости сводится с молекулярно-кинетнческой точки зрения к трансляционному движению ионов и молекул воды в направлении действия приложенной силы (А>р). В данном случае такой силой будет

где Uki - сила Лоренца.

Будем считать жидкость механической системой, состоящей из независимых частиц (ионов) и молекул воды, находящихся в тепловом движении. В этом случае импульс системы Р аддитивен и равен в единицу времени

Р=Е Z miVife = MVe.