объемной вследствие наличия поверхностной проводимости слоя жидкости, прилегающей к стенкам капилляра. Изменение электрической проводимости вблизи стенок связано, во-первых, с изменением концентрации носителей в диффузной части двойного слоя по сравнению с их концентрацией в жидкости и, во-вторых, с тем, что при прохождении тока сам раствор движется, причем вместе с жидкостью перемещаются и заряды обкладки двойного слоя.

При движении частиц в жидкости (газовых пузырьков, ртутных капель) возникает седиментационный потенциал, т. е. разность потенциалов в растворе, обусловленная движением диффузных двойных слоев частиц.

Выражения (2.1) и (2.2), обычно используемые в физической химии, в значительной степени условны и ограничены рядом допущений. Так, например, рассматривается случай лишь ламинарного потока, в то время как в реальных пористых средах с переменным радиусом сечения обычно имеет место турбулизация потока при низких Re l-5. Кроме того, вывод (2.1) проводится для случая, когда поток принято считать установившимся, стационарным, и сила возникающего омического тока полностью ком-пенснрует /т. Явление компенсации заряда в капиллярах может отсутствовать в том случае, когда капиллярная трубка имеет диаметр 0,2-1,0 мкм и сопротивление для тока утечек становится весьма значительным, так как площадь поперечного сечения канала S~10~° см2, /?к~3-10 Ом [90]. Чем длиннее капилляр /, тем больше Rk и компенсация тока за счет омических потерь /о ниже. Следовательно, с увеличением активного сопротивления в капилляре увеличивается время релаксации в электролите объемного заряда, уносимого потоком.

Жидкость заряжается выходя из капилляра или диафрагмы, при соотношении Го-С/, го-бдв и может выносить значительный электрический заряд: /т<10- А при плотности разделенных зарядов не выше 5-10 Кл/см.

Теоретические вопросы возникновения электрических, магнитных и динамических явлений при фильтрации электролита в капиллярно-пористых системах рассмотрены в цикле работ [24].

Одной из первых работ, где отмечается необходимость связи гидродинамического режима в пористой среде с объемными электрическими зарядами, возникающими в потоке электролита, является [158]. В ней рассмотрены два случая стационарного нарушения электронейтральности в потоке: из-за геометрии канала и шероховатости стенки (рис. 2.1). Возникающие вихревые потоки могут уносить объемные заряды на значительные расстояния, так как для подобной геометрии систем можно ожидать (вследствие значительных перепадов давления) возникновения вихреобразо-вания, а при определенных скоростях и турбулентности.

Одиночный капилляр. Движение жидкости в капиллярах с проницаемыми стенками представляет особый интерес при решении задач химической физики, биофизики и медицины.

Рассмотрим капилляр радиусом гол (рис. 2.2), приняв цилиндрическую систему координат п, уи ф1 с центром Оь При ух /i (область I) стенки капилляра будем считать непроницаемыми, а при г/1 /i - проницаемыми (область П). Радиус пор го.2<го.1, тц -вязкость жидкости в капиллярах, TI2 -вязкость жидкости в порах, то.2, к - предельное напряжение сдвига жидкости в капиллярах, То,2, п - предельное напряжение сдвига жидкости в порах.

-

+j- +J-+ + ++><#%:-+>-+-+-+-+-+ i

Рис. 2.1. Схема, иллюстрирующая возникновение свободных электрических зарядов в потоке при различной геометрии по [158].

а - выход потока из трубки в объем жидкости; б - шероховатость на стенке. 7 -твердая стенка; 2 -жидкость; 3 - положительно заряженный слой; 4 - отрицательно

заряженный слой жидкости.

Рис. 2.2. Схематическое изображение капилляра с проницаемыми стенками.

Область / - стенки капилляра непроницаемы, - стенкн капилляра проницаемы.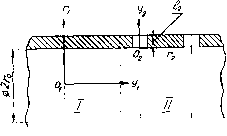

Гидростатическое давление вне капилляра и в капиллярах примем р. Число пор на 1 см2 поверхности о, причем о > 1, /2 -толщина стенок капилляра, U<1\. Движение электролита обусловлено начальным давлением

Р0 = р0 - 2То.2,к1/Го.1,

(2.3)

где Ро - приложенное внешнее давление, а член 2то.2, ki/ro.i учитывает пластическое сопротивление сдвига жидкости.

Систему уравнений Навье-Стокса и непрерывности (1.23) в цилиндрических координатах для области II с учетом того, что VrO, др/дгфО, можно представить в виде

-др/ду + цАУу = 0 [ (2.4)

дУг/дг + Уг1г + дУу1ду=о\

Достаточно точное решение системы (2.4), даже с учетом того факта, что инерционностью среды можно пренебречь, представляет большие математические трудности, и до настоящего времени практически отсутствуют работы по движению жидкости через стенки с учетом геометрических параметров системы и физико-химических свойств жидкости. Не учитывались различия в структурных особенностях свойств жидкости в столь различных объемах, как сам капилляр и его поры, хотя соотношения радиусов обычно Го.-/гал<.\.

Феноменологическое уравнение Навье-Стокса, выведенное без учета микроскопических свойств жидкости, не позволяет провести подобные исследования.

Учитывая все это, для получения Vr в зависимости от геометрических и физико-химических параметров системы был использован следующий прием. В области П при y\>li введена новая система координат Г2, г/2, Ф2 с центром Ог, расположенным в нижней части одной из пор, с координатами г = го,и ф = 0. Новая система связана с системой координат Гь г/ь ф1 следующим образом: так как ось г/2 соответствует гь то Vr соответствует Vy в рассматриваемом случае

др1дг-=др1ду\ Рпр:Фр р2-

Отметим, что в общем виде цФц, рпх,\фрпх>2- При г/2 = 0 р определяется выражением (2.3); Уу = 0 при О р Рпр2, Рпр 2 = 2x0.2 ahlro.2. При 2/2 = 2 Р=Ро.1- Начальные условия: Vy=(i при >2 = го.2, дУу,1ду2=0 при Г2=0. Следовательно, можно записать

У;, = -{г1218ц2)др1ду,. (2.5)

Принимая во внимание, что рассматривается перепад давления только на стенке капилляра и так как h<l\, вполне корректно в данном случае уравнение

др1ду2 = (ру - ро - Рпр.2)Л2. (2.6)

Таким образом, среднее значение скорости в порах капилляра

Скорость движения электролита через участок с проницаемыми стенками увеличивается с увеличением диаметра пор, с уменьшением толщины стенки и вязкости (п - коэффициент, больший единицы).

С увеличением г/ь т. е. с удалением рассматриваемого участка с проницаемыми стенками от места генерации, давление падает и Vr уменьшается. Vr зависит от то.гк и то.2п, т. е. от реологических свойств жидкости и от характера падения давления по длине капилляра.

Поскольку получение д{г) в явной форме для данного случая достаточно сложно, то ограничимся использованием общего вида для объемного заряда qirz) в порах.