ГЛАВА I

ЭЛЕМЕНТЫ РАДИОТЕХНИЧЕСКИХ ЦЕПЕЙ И ИХ ОСОБЕННОСТИ ПРИ ВЫСОКОЙ ЧАСТОТЕ,

ОБОЗНАЧЕНИЯ К ГЛ. I.

А-В-С-Сг

с D-

Е,е-Е-

е F Н-

Л-/, I

In-М М т -Р

Q R,r

работа,

магнитная индукция емкость

емкость на единицу длины скорость света

электрическая индукция

расстояние

напряжение, разность потенциалов сила (напряженность) электрического поля

- основание неперовых логарифмов

сила

сила (напряженность) магнианого поля

расстояние

- сила тока

мнимое число У-1 (оператор поворота вектора на угол

коэфициент самоиндукции

- коэфициент самоиндукций на единицу длины

- расстояние

- натуральный логарифм

- магнитодвижущая сила

- коэфициент взаимной индукции

- масса

- мощность

- заряд

- активное (ваттное) сопротивление -диэлектрическое сопротивление

- магнитное сопротивление

- радиус

t - время и - потенциал V - скорость W - энергия

Z-комплексное выражение кажущегося сопротивления (Z - r-jx) 7 - удельная проводимость S - диэлектрическая проницаемость (Л - магнитная проницаемость S - угол потерь Ф - поток силовых линий О), Q - круговые частоты = - знак тождества. Выражение (а -\- Ь)с означает: обозначим (а Ь) через С. Амплитудные значения переменных величин обозначены большой буквой с индексом т, например, Е, и т. д.

Постоянные и среднеквадратичные значения-теми же буквами без индекса, например Е, I, Р и т. д.

Мгновенные значения, выраженные в тригонометрической форме, обозначены малыми буквами, например,

/ = sin (oit) и пр.

Мгновенные значения, выраженные в комплексной форме, обозначены большой буквой с точкой наверху, например,

i = a+ jb, QJii+P) и пр.

§ 1. Статическое электрическое поле.

Электрическим полем называется пространство, в котором проявляются электрические силы взаимодействия. Если в электрическое поле внести заряд, то этот заряд испытывает механическую силу, стремящуюся перемещать его в некотором направлении. Это направление называется направлением электрической силы в данной точке пространства.

Поле характеризуется величиной и направлением электрической силы. Величина электрической силы Е численно принимается равной механической силе F, которую испытывает в данном поле единичный положительный ааряд, сосредоточенный в одной точке.

Так как электрическая сила определяется величиной и направлением, то она изображается вектором Е. Следует заметить, что название электрическая сила представляет собой термин, который не надо понимать буквально: электрическая сила ни по своей природе, ни по своей размерности не является силой в механическом смысле, и только определяется путем измерения механической силы, с которой поле воздействует на заряд.

Статическое электрическое поле (т. е. такое, которое мы наблюдаем в неизменяющемся состоянии) заканчивается на электрических зарядах. Поэтому часто говорят, что это поле образуется зарядами .

Электрическое поле является основой всех электрических процессов. Пока электрическое поле существует в неизменном статическом, состоянии, никаких электрических явлений не происходит. И, наоборот, всякое электрическое явление связано с изменением, т. е. с убыванием, нарастанием или движением электрического поля в той области пространства, в которой происходят электрические явления.

Для описания и изображения поля удобно пользоваться представлением о силовых линиях (или силовых трубках). Направление силовой линии характеризует направление, а густота (т. е. число линий на квадратный сантиметр нормального сечения) характеризует величину так называемой электрической индукции , которая в пустоте равнозначна с электрической силой, а в диэлектриках

связана с электрической силой соотношением

eE = D,

(1.1)

Фиг. 1.1.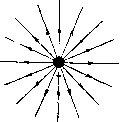

Фиг. 1.2.

где 5 некоторый коэфициент, зависящий от вещества, заполняющего пространство. Он называется диэлектрической проницаемостью среды .

Число силовых линий, испускаемых единичным зарядом, принимается равным 47г, так что, если заряд Q равномерно распределен по поверхности шара радиуса г, то на поверхности шара на каждый квадратный сантиметр приходится

В = диний. (1.2)

Полное число силовых линий, пронизывающих какой-нибудь контур, называется потоком индукции через этот контур. Так например, на фиг. 1.1 совокупность силовых линий проходящих внутри кольца А, образует поток Ф, пронизывающий это кольцо; все остальные линии не входят в данный поток, ограниченный кольцом.

В однородном пространстве поле точечного заряда изобразится линиями, радиально расходящимися из центра (фиг. 1.2).

Всякое поле можно представлять как результат сложения радиальных полей, образованных элементарными положительными и отрицательными зарядами.

Результирующее поле нескольких зарядов получается путем векторного сложения электрической индукции D в каждой точке пространства.

Так например, на фиг. 1.3 показаны два радиальных поля. Стрелками, поставленными на линиях поля, обозначено направление электрической силы. В случае положительного заряда эта сила направлена от центра, а в случае отрицательного - к центру.

Если в какой-нибудь точке пространства существуют две равные электрические силы, направленные противоположно, они уничтожают одна другую, и результирующая сила поля равна нулю.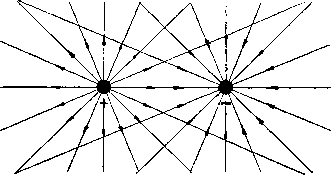

Фиг. 1.3.

Если электрические сиЛы (или электрические индукции), образуемые двумя зарядами, направлены под углом, то результирующая сила (или индукция) получится как равнодействующая этих двух слагающих.

Изображая обе электрические силы векторами Ei и t, найдем результирующую электрическую силу по правилу параллелограма, как это, например, показано на фиг, 1,4, То же самое относится и к векторам электрической индукции D,

На фиг. 1.5 показан результат такого сложения полей, изображенных на фиг. 1.3.

Такое сложение полей основано на применении принципа суперпозиции. Оно может производиться только в случае линейной среды, т. е. когда диэлектрическая проницаемость е не зависит от индукции.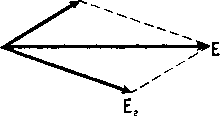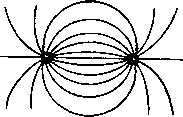

Фиг. 1.4.

Фиг. 1,5.

Результирующее поле вокруг заряженного шара при равномерном распределении зарядов на его поверхности совпадает с полем точечного заряда.

Такие построения можно применять только в тех случаях, когда распределение зарядов может считаться известным.

Если заряды расположены на проводнике, то обычно их распределение Иельзя считать правее известным, так как оно в свою очередь зависит от результирующега поля, под влиянием которого заряды могут перемещаться по поверхности проводника. В этих случаях указанным построением пользуются дляполучения приблизительной картины поля.

§ 2. Электрический потенциал.

В однородном пространстве линии поля расходятся от заряда радиально.

Окружим заряд сферой так, чтобы он был расположен в центре. Так как число линий остается неизменным , а поверхность сферы, которую они пересекают, пропорциональна квадрату радиуса, то очевидно, что число линий, приходящихся на 1 см нормальной поверхности, уменьшается пропорционально квадрату расстояния.

Математически это запишется следующим образом

0 = ..

Отсюда

D Q \ .

е г

(1.3)

(1.4)

Если в поле поместить точечный заряд Qi, он испытает силу, равную EQi, откуда следует, что

Q 1

(1.5)

Эта сила направлена по линии, соединяющей центры зарядов. Если заряд Qi перемещать по направлению силы F (т, е, к центру или от центра поля Q), то будет совершаться нкоторая работа .4.