Наконец, если получим

Zj = Z2 - Zg - Z4

1 ~~ 8Z

ЗЁ1 8Z

8 Z

-А 8Z*

Если элементов не 5, а 4, то полагают, например Zj (или другое Z) равным нулю. Этим путем иногда удается привести схему к лестничному виду.

Фиг. 9.

Для схемы, содержащей семь элементов (фиг. 9)

- fijUe -f 7} {Z5(Z3 + Z,) + Z,Z,} + Z,Z;(Z3 -f-ZJ].

= EiZilJZ, +Z,)(Z,-\-Z,) + Z,Z,], H

£iZ2[Zs(Ze+Z,)-f-Z,Z,]. H

~ H

EiZfZfZ.,

~ H

= EiZtZZf, H

H = {Ze + Z,} {Z,iZ, + Z3)(Z, + Z3) + Z,ZiZ, + Z,) + Z.ZCZi + ZJ} + + ZeZ, {(Zi + zj (Z3 + z,) + Z,Z,}.

На фиг. 10 показаны две схемы так называемого мостового типа. Все эти схемы совершенно идентичны и различаются только способом изображения.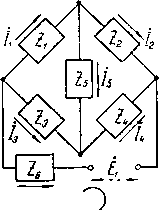

Фиг. 10.

Для них имеем следующие формулы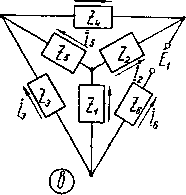

/ - 4[25(2з + 24) +24(Zi + Z3)] ,

£i{Z,(Zi-f Z2>+Zi(Z2 +Z,)] , Н

г EjjZZ Z1Z4)

/ E,[ZdZ, + Z,) + {Z,-\-Z,)(Zxi Z, + Z,)]

Н - (Zj + Z2) (Z3Z4 + ZgZe) -f (Z3 + ZJ (Z1Z2 + ZZe) -f (Z, -f Z) (ZjZ, + Z2Z3) -f + Z,(ZiZ3 + Z,Z,) + Z,{Z,Z, + Z3Z,).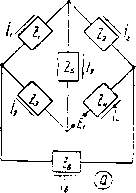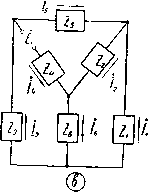

На фиг. 11 показаны те же мостовые схемы, но источник эдс включен в одно из плеч моста Два варианта начертания а и b изображают одну и ту же схему

E,[Z,iZ, + Z,) 4- Z,(Z,-{-Z,)] , ~~ Н

- Ex[Z,(Z, 4- Z,) Ч- Z,(Z, + Ze)] , ~ Н

- iJZxiZ, + Z,) (Z, 4- Z,) (Z, + Za + Z,)] ,

E,[Z,(Z,+Z,)-{-Z,{Z,-bZ,)] , Н

Е, [Zi(Zg Ч- Z J Ч- Z2(Z3 -f Z J] ,

Н ~ (Zi + Z,) (Z3Z, + Z,Z,) -f (Z3 -I- Z,) (ZiZa -f ZZe) -f (Z5 + Z,) (Z.Z, -f Z,Z3) + -b ZiZiZ3 + Z,Z4) + ZeiZ.Z, -f Z3Z,).