
 |
|
|
Главная -> Основание неперовых логарифмов Коэфициент К находится из следующей табл. V/.
3) Две круглые однослойные катушки с числом витков Щ и п расположенные коаксиально (фиг. 2). Буквенные обозначения на фиг. 2 соответствуют обозначениям в формуле М = 0,62 ЩП (К А + ККг), 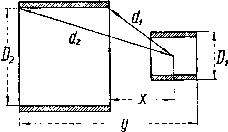 где li - длина малой катушки, а /g -Длина большой катушки Фиг. 2. ПРИЛОЖЕНИЕ IV. Формулы для лестничных и мостовых схем. Многие схемы могут быть приведены к виду так называемых лестничных схем. Пример начертания лестничной схемы показан на фиг. 3. Здесь под Zi, Zo... подразумеваются те, либо другие комплексные сопротивления. -I Z, <-.-~zT ,-,- Z. I-f-I I-- Фиг. 3. 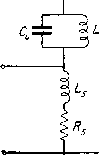 при этом на первый взгляд схема может и не иметь вида, при котором расположение элементов напоминало бы лестничное расположение. Так например, схемй фиг. 4 вовсе не напоминает схемы фиг. 3 по своему построению. Однако ту же самую схему можно например, начертить так, как, показано на фиг. 5, и тогда она получает характер лестничной схемы. Удачное расположение элементов сложной схемы, выявляющее ее смысл, является очень важным моментом как для расчетов, так и для понимания действия схемы. Мы выйишем здесь ряд формул для лестничных схем с различным числом элементов. Для того чтобы пользоваться этими формулами, надо прежде всего придать схеме лестничный характер, стремясь к тому, чтобы представить данную схему в виде ле- Фиг. 4. г 1 * с * ) L i 2 СТНИЦЫ с наибольшим количеством ступеней. Далее обозначают на действительной схеме стрелками направления токов так, как они указаны на той типичной схеме, которой пользуются. После этого взамен Zj, Za и т. д. подставляют в данную формулу действительные значения комплексных сопротивлений и находят токи /j, /3 и т. д., текущие через весь элемент Z в целом. После этого легко найти интересующие значения токов и напряжений для любого участка относительно простой цепи, которая была обозначена как Z . На фиг. 6 показана схема, содержащая три элемента. Соответствующие ей уравнения будут Фиг. 5. /1 = ZZ ~}~ ZjZ -EZ, Ze,Z<) ZlZ -j- ZjZg -f- Z2Z3 Фиг. 6. E Zg ZjZg -j- ZZi -j- z2z3 Положим, что написанными формулами хотят воспользоваться для определения напряжения между точками Л и В в схеме фиг. 7. Так как Zi==/<bLi; Z2 = Zg = /{OL2, то пишем /з = £х Далее = Я1 Фиг. 8. Для лестничной схемы, показанной на фиг. 8 и содержащей пять элементов, токи определяются следующими формулами / ~ Ex[{Zi+Z,){Z, ±Z)±Z : Ex[Z,{Z,-i-Z,)-Z,Z,] h- H V iZgZg 4--Ff- / , £1224 5 = - н=Zi(Z2+Z3) (Z4++z.zczi+Z2) 4- z,z,(z,+Z5). Если Zi = Z3 = Z5 и в свою очередь Z2=Z4, то получим 1 E,[iZ,-\-z,y+ZxZ] ---- v E,[Z,{Z, + Z,) + ZxZ,] 1--- h--. и--H - , p 7 г H H = Zi(Zi + Z,)2 + 2ZiZ,(Zi + Z2).
|