Из интеграла Фурье можно получить уравнение этой огибающей в форме

i=F(S). (0.59)

В этом выражении dA представляет собой бесконечно малую амплитуду, соответствующую частоте Q, а делитель dQ появляется потому, что по мере уменьшения интервала между частотами (с увеличением Т) мы изменяем вертикальный масштаб чертежа.

Таким образом мы получаем возможность охарактеризовать спектр, в котором интервалы между частотами бесконечно малы. Такой спектр называется сплошным спектр,ом.

Для того чтобы охарактеризовать функцию как в отношении амцлитуд, так и в отношении фаз, надо построить два сплошных спектра, один для синусов, другой для косинусов.

Обычно, однако, прибегают к другому способу и чертят одну кривую для амплитуд, а другую для фаз, что также исчерпывает всю картину. Часто впрочем фазовая кривая не представляет большого интереса для практических целей.

На фиг. 0.30 приведены три кривых, соответствующих ур-нию (0.59) для затухающей синусоиды, выражаемой уравнением

О при /<0

Ет sin ((Df) е- при f > О

Три кривых соответствуют трем различным значениям отношения -, указан-

(0.60)

J3

Vi2 Фиг. 0.30.

НЫМ на чертеже.

Приведенные кривые показывают, что чем меньше затухание, определяемое

значением-, тем больше увеличение

амплитуды вблизи района, где Йш.

Следует обратить особое внимание на то, что ординаты этих кривых

выражают значение величины Амплитуды же представляют собой бес-

конечно малые величины

, dQ = dEm, стремящиеся в пределе к нулю.

Иными словами, в случае сплошною спектра амплитуда колебания для всякой дискретной частоты равна нулю.

Поэтому, если бы был построен прибор, который мог бы реагировать только на определенные дискретные частоты, он не получил бы никакой энергии от источника, дающего сплошной спектр.

Если же прибор воспринимает полосу частот от Q до Q-\-dQ, то действие источника будет пропорционально площадке, заштрихованной на

фиг. 0.30, имеющей высоту и основание dQ.

Фактически мы всегда имеем дело со сплошными спектрами вследствие того, что реальные физические процессы не выражаются периодическими функциями в математическом смысле. С другой стороны (как будет показано), нельзя построить физического прибора, который реагировал бы только на дискретные частоты, а не на некоторую полосу сплошного спектра вблизи определенных частот.

Поэтому линейчатый спектр представляет собой приближенное выражение реального спектра.

В действительности то, что мы называем спектральной линией, пред сталяет собой только резко выраженную вершину кривой сплошного спектра, ординаты которой быстро убывают по мере удаления от данной частоты.

JCneKTp можно называть линейчатым, поскольку он представляется нам таким в пределах точности наших измерений или если такое упрощение не играет роли для поставленной задачи.

При увеличении требований со стороны точности линейчатый спектр представляется нам полосовым .

Отрезку синусоиды, длящейся п периодов, соответствует сплошной спектр, характер которого показан на фиг. 0.31.

При увеличении числа периодов в отрезке синусоиды центральная часть кривой (вблизи частоты ш) становится уже и выше, в то время, как вторичные максимумы при частотах < + (где К=1, 2, 3...) становятся

меньше. При п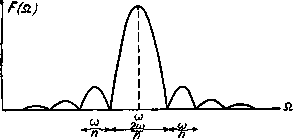

Фиг. 0.31.

оо основной максимум при основной частоте стремится к бесконечности, а кривая стягивается в одну вертикальную линию.

§ 14. Трансформация спектров

при посредстве линейных систем.

Сопротивление линейной электрической цепи вообще зависит от частоты. Если в цени отсутствует эдс сложной формы, то ее можно представить как спектр частот и для каждой частоты найти ток, соответствующий эдс при этой частоте. Эти токи будут находиться в различном соотношении к отдельным эдс.

Так например, если для эдс ei при частоте оО] сопротивление цепи было

а для эдс 2 при частоте ( а сопротивление было ТО ток, образованный первой эдс, будет

а ток, образованный второй эдс, будет Таким образом

7 е г.

4-ii

(0.61) (0.62)

(0.63) (0.64)

(0.65)

Ур-ние (0.65) показывает, что отношение между токами равной частоты не равно отношению между соответствующими напряжениями, и угол сдвига фазы между токами отличается от угла сдвига фазы между эдс.

Совокупность всех токов образует спектр токов, которому соответствует та либо другая кривая формы тока.

Из сказанного ясно, что если Z величина постоянная, то спектр, этой кривой не может содержать никаких новых частот. Такое же положение буде¥, разумеется, иметь место и в том случае, если от тока перейти к напряжению на каком-либо участке цепи.

Спектр этого напряжения будет содержать те же частоты, что и спектр действующей в цепи эдс, но в смысле фаз и амплитуд он может как Угодно отличаться от спектра эдс.

Это правило выражает существенную особенность линейных систем с постоянными параметрами (т. е. с неизменяющимся во времени соцроти-влением Z>. Оно формулируется так: л инейные системы могут трансформировать спектр в отношении частот и амплитуд, но не могут создавать новых частот.

Уничтожение существующих частот, т. е. доведение их амплитуд да нуля, согласно этому правилу возможно, но для этого требуется, чтобы цепь обладала для этих частот бесконечным сопротивлением при переходе от напряжения к току или чтобы сопротивление равнялось нулю при переходе от тока к напряжению.

Выделение одного сигнала на фоне других сигналов возможно только в том случае, если спектры этих сигналов различны.

Основной метод, который применяется в радиотехнике для разделения сигналов, как раз и использует отмеченное здесь свойство линейных систем.

При помощи электрических цепей из всей массы принятых сигналов выделяются желаемые сигналы путем увеличения амплитут тех частот, которые составляют этот сигнал, и уменьшения амплитуд тех частот, которые образуют все остальные мешающие сигналы.