Чем меньше di, тем выше качество катушки в смысле потерь.

На практике при высоких частотах удается получить di порядка 0,003.

Это облегчается большим значением (о, стоящей в знаменателе правой части ур-ния (6.28), несмотря на то, что с другой стороны скинэффект и повышает зйачение R.

При частотах ниже 100 гц получение £==0,03 уже становится затруднительным.

Обычно для фильтров применяются катушки, имеющие di от 0,003 до 0,02 в зависимости от требуемого совершенства фильтрации и частоты. За меру качества конденсаторов принимается величина

dc==<aCr,

где г эквивалентное сопротивление, присоединенное параллельно конденсатору.

Потери в конденсаторах при низких частотах весьма малы и при слюдяных конденсаторах dc обычно меньше 0,001, вплоть до частоты порядка IQb jpjj брлее высоких частотах потери значительно возрастают,

как об этом подробно было сказано в гл. I.

При частотах порядка 10-10 гц и выше потери в слюдяных конденсаторах могут уже превышать потери в катушках. В этом случае для фильтров высокого качества применяют или конденсаторы с специальными диэлектриками с малыми потерями, или воздушные конденсаторы.

Тем не менее потери никогда не могут быть сведены к столь низкому уровню, как при низких частотах, так как кроме потерь в диэлектриках при очень высоких частотах часть энергии рассеивается вследствие емкостной связи с окружающими элемейтами.

§ 25. Затухание, вносимое отражением.

До сих пор мы предполагали, что звенЪ фильтра замкнуто на сопротивление, равное его волновому сопротивлению. В действительности волновое сопротивление фильтра, как известно, зависит от частоты, в то время, как сопротивление нагрузки может представлять собою чисто активное сопротивление R. Поэтому в реальных цепях нельзя получить точного согласования между фильтром и нагрузочными цепями. Это приводит к тому, что в точках присоединения нагрузки получается отражение.

Амйлитуды тока и напряжения в этом случае могут быть и больше и меньще, чем в случае согласованного сопротивления, в зависимости от устройства фильтра и от величины нагрузки.

Вследствие отражения фильтр получает положительное или отрицательное затухание в пределах той полосы частот, которая при согласо- Фиг. б.64. ванной нагрузке являлась полосой прозрачности.

Выясним зависимость отражения от величины включенного сопротивления. Положим, что источник эдс замкнут на нагрузку и имеет внутреннее сопротивление (фиг. 6.64). Тогда ток в цепи будет

(6.29)

Если сопротивление Z и Z равны между собой, то

(6.30)

ур-ние (6.30) соответствует согласованному соединению источника и внешнего сопротивления Z, а ур-ние (6.29) -несогласованному.

Положим, что, имея различные и Zg, мы вводим между зажимами источника и сопротивлением идеальный трансформатор, посредством которого сопротивление Zg трансформируется в сопротивление Z.

Такой трансформатор согласно § 22 должен обладать коэфициентом трансформации

Ток в цепи источника определится ур-нием (6.30), а ток /2 в цепи на-/ z7

грузки будет в I/ 27 Р больше.

Так что

2 2YZxZ

(6.31)

Отношение тока

2 Z1 + Z2

который протекает при несогласованной нагрузке, к току /3 , определяемому ур-нием (6.31), обозначим буквой D. Это отношение называется фактором

отражения

2 Yz,z, Zx + z,-

В случае фильтра сопротивление Z является волновым сопротивлением фильтра, а Z2 - сопротивлением нагрузки.

Величина, обратная фактору отражения, т. е.

1 Zi + Z2

D 2/Z

является мерой эффективности передачи при непосредственном соединении звеньев цепи с различными сопротивлениями Zj и Z2 сравнению с согла- . сованным соединением, если согласование достигнуто путем трансформации Z2.

Так как величина является вообш;е комплексом, то ее можно пред-

ставить как

Zi+Z,

2VZ,Z,

является мерой перехода мощности в на-= 1,

Квадрат амплитуды грузку. При Zi = Zg

т. е. затухание по мощности равно нулю. В других случаях отражение может привести как к уменьшению, уак и к усилению перехода мощности, т. е. затухание может быть и больше и меньше нуля, и сможет быть определено по формулам

20 Ig

Zx-f-Z 2 JZ.Z

Nnen == In

z,+z,

2VZ,Z,

На фиг. 6.65 показаны кривые, дающие затухание вследствие отражения в зависимости от отношения модулей двух последовательно включенных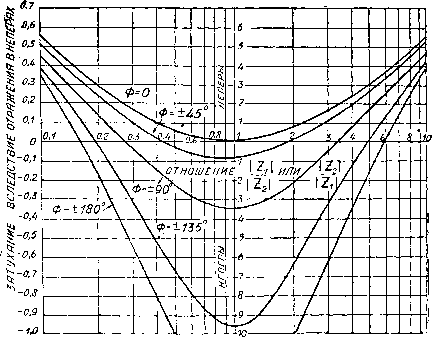

Фиг. б.65.

сопротивлений IZilnlZg] (фиг. 6.66). Цифра 1 на оси абсцисс соответствует случаю

Zil = lzH.

Правее этЪй точки Левее

\Zx\<\Z,\.

Для того чтобы пользоваться этими кривыми, кроме отношения модулей, надо знать угол Ф. Для этого надо разделить Z на Z и представить полученный результат в форме мнимой степени

Zx

= Ле.

Фиг. 6.66.

Каждая кривая соответствует своему углу Ф. Случай

ф = 0 соответствует случаю, наиболее нас интересующему, когда фазовый угол между комплексами Z и Z равен нулю. Это значение Ф имеет в полосе прозрачности фильтра при условии, что фильтр нагружен чисто активным сопротивлением, которое (как это всегда бывает) не равно волновому сопротивлению фильтра в пределах всей полосы прозрачности.

При несогласованности волнового сопротивления фильтра с сопротивлением присоединенных к нему цепей не только на входе, но и на выходе отражения имеют более сложный характер. В этом случае отражение имеет место в обоих точках перехода; кроме того, волны, отраженные от одного конца, вновь отражаются от другого.