в следующей таблице сопоставлены формулы для полосового фильтра с формулами для фильтра низкой частоты.

§ 17. Режекторный фильтр.

В полосовом Т-образном фильтре последовательные плечи состоят из последовательно соединенных емкости и самоиндукции, а -параллельные - из параллельно соединенных емкости и самоиндукции. Если эти элементы поменять местами, получится схема фиг. 6.38. Фильтр, составленный из таких звеньев, имеет области пропускания по обеим сторонам некоторой

тлпгч

Фиг. 6.38.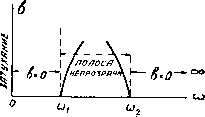

Фиг. 6.39.

ПОЛОСЫ, в пределах которой получается затухание. Характеристика его показана на фиг. 6.39. Он носит название полосового запирающего фильтра или режекторного фильтра .

Воспользовавшись аналогиями, указанными в § 15, последовательные плечи этого фильтра можно рассматривать как емкостные, а параллельные- как индуктивные. Другими словами, в том же смысле, в каком полосовой фильтр соответствует фильтру низкой частоты, этот фильтр соответствует фильтру высокой частоты.

Поэтому можно прямо написать величины, относящиеся к этому фильтру, заменив в выражении для фильтра высокой частоты С ria Ci, L на Lg, а> на (coj - СО2).

Получим следующую таблицу.

Таблица VI.IIl

Фильтр высокой частоты

Режекторный фильтр

пред 4LC

(0)1

С 4w?C2

Cl 4(o>i-toa)Cf

b = arcch(Ai)

& = arc ch (Aj)

2 1 1

oJq -- ~-

§ 18. Фильтры с несколькими полосами прозрачности.

Если в полосовом фильтре рассмотренного типа ЬхСхф LCi, то изменение Aj с частотой выражается кривой фиг. 6.40. Вершина этой кривой заходит выше уровня Ai==l. Поэтому получаются две полосы прозрачности а - b и с - d, и между ними- полоса затухания Ь-с.

Могут быть также образованы фильтры и типа постоянной к, в которых имеется несколько полос прозрачности.

Так например, схема, показанная на фиг. 6.41, позволяет получить три полосы прозрачности. Характеристика его показана на фиг. 6.42.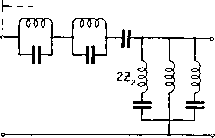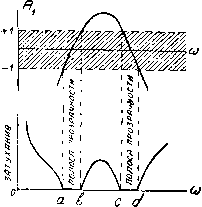

Фиг. 6.40.

Фиг. 6.41.

Фиг. 6-42.

§19. Фильтры типа т.

Фильтры типа к обладают относительно малым затуханием в области, близкой к полос-е прозрачности. Казалось бы, что для увеличения затухания вблизи полосы прозрачности, или в других областях, можно включить в звенья- типа к, запирающие и короткозамыкающие контуры.

Например, на фиг. 6.43 показано последовательное включение в звено простого фильтра низкой частоты контура LjCi, запирающего частоты

I------- вблизи а)2==-г, или параллель-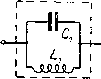

2 L 2L

, 4mjL

вблизи = -ij>

ное включение контура, короткозамыкающего т£ же частоты.

Фиг. 6.43.

Фиг. 6.44.

Однако при таком включении произвольно взятых контуров волновое сопротивление и полоса прозрачности вообще изменятся.

Если ставится требование к сохранению этих параметров неизменными, то включаемые новые элементы должны удовлетворять особым, условиям, которые мы здесь выясним.

Рассмотрим полузвено фильтра, схема которого показана на фиг. 6.44. Волновое сопротивление его со стороны зажимов аЬ равно

(6.26)

(Заметим, что ~--сопротивление при коротком замыкании зажимов cd;

Zx-\-2Z - при холостом ходе, т. е. при полном размыкании зажимов cd).

Изменим сопротивление плеча в яг раз и посмотрим, что надо

сделать с плечом 2Z2 для того, чтобы сохранить прежнее значение волнового сопротивления.

Прежде всего очевидно, что для того, чтобы произведение под знаком

корня в ур-нии (6.26) осталось неизменным, надо в раз увеличить сумму (iz, + 2Z,).

Таким образом в измененном звене сопротивление короткого замыкания

\k (от) - J а сопротивление холостого хода

7 Zj I 2Z2

Для исходного полузвена можно написать

Zjp - Zjft = Zj-f- 2Z2- Z = 2Z2.