Поэтому предельная частота равна

......V

гфед

4LC S

папосй прозРйчности ----- оо

Фиг. 6.31.

Фиг. 6.32.

Волновое сопротивление этого фильтра легко найти, определив по таблицам коэфициенты Ag и Ag. Получим

\ к. Ус 4(о2Са-

Аз Г С

§ 14. Полосовой фильтр типа к.

Фильтр, схема которого показана на фиг. 6.33, также принадлежит к фильтрам постоянной к, если

Действительно, в этом случае произведение сопротивлений плеч будет

С, *

Характеристика затухания этого фильтра показана на фиг. 6.34. Из этой характеристики видно, что фильтр имеет полосу прозрачности, ограниченную областями затухания. Поэтому он называется полосовым фильтром.

21 4rL 2С,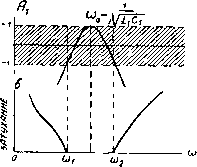

Фиг. 6.33.

Коэфициент Ai для данной схемы будет A,= l+ = l + l(o)L,

Фиг. 6.34.

(6.17)

Характер изменения Ai с частотой а> показан на той же фиг. 6.34 сверху.

Предельные частоты oi и могут быть определены на основании ур-ния (6.17), положив

Непосредственное решение связано с громоздкими вычислениями. Поэтому мы укажем сначала упрощенный прием, применение которого полезно и в других случаях.

§ 15. Аналогия между элементами

полосового и низкочастотного фильтра.

Для цепи, образованной последовательным соединением емкости и самоиндукции (фиг. 6.35), при частоте (Oj можно написать

о-ПППЯЯР-II-1,

II в зависимости от значения (Oj, х может

Фиг. 6.35. быть положительным или отрицательным.

Возьмем другую частоту cog и подберем ее таким образом, чтобы значение х по абсолютной величине было бы равно его значению при частоте (Oi, а по знаку - обратно. Тогда

= ( -) = -( -=> (6.18>

Обозначим

и перепишем ур-ние (6.18) так

оЧ-) = - Ч-)- (6.19)

Разделив обе части на %L и перекомбинировав члены в ур-нии (6.19), получим

(Dj -j- 2 + 2

откуда очевидно, что

l/i; = coq. (6.20)

Ур-ние (6.20) показывает, что частота резонанса (о является средним геометрическим между любой парой частот со и при которых х имеет одинаковое абсолютное значение, но противоположные знаки.

Из ур-ния (6.20) имеем

Подставим это в равенство получим

= G:-)=(< i-°)i- (6-21)

ур-ние (6.21) дает следующий замечательный результат.

Формула для определения сопротивления цепи из последовательной емкости и самоиндукции имеет тот же вид, как и формула для определения индуктивного сопротивления ((oL) с той только разницей, что вместо частоты множителем при L стоит разность частот и о), связанных между собой равенством

Совершенно аналогичная формула получится и для параллельного со-

единения емкости и самоиндукции (фиг. 6.36). В этом случае

1=< ,С--L = (,C-JL).

(6.22)

сравнив ур-ние (6.22) с ур-нием (6.18), можно сразу написать окончательный результат, заменив х на и поменяв С и L местами. Получим

1

~( 1-о>,)С-

(6.23)

Эти аналогии позволяют чрезвычайно упростить вычисления в сложных цепях. Мы ими воспользуемся для-исследования некоторых фильтров.

Фиг. 6.36.

§ 16. Вычисление параметров полосового фильтра посредством аналогии с низкочастотным фильтром.

На основании указанных в предыдущем параграфе аналогий звено полосового фильтра приводится к следующей эквивалентной схеме (фиг.6.37). По таблицам коэфициентов четырехполюсника легко получим

7 = -

(6.24) (6.25)

Фиг. 6.37.

Ур-ние (6.24) дает возможность определить предельные частоты фильтра.

Непосредственно видно, что если, например, a)i = a)o, то, так как в этом случае и 0)3 = 0)0, Ai=l.

На графике фиг. 6.34 этому соответствует вершина кривой Ai = /(o)). Для того чтобы Aj было равно минус единице, надо, чтобы было выполнено равенство

(со - 0)3)