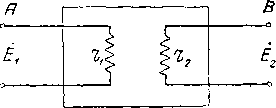Фи1. 6 17.

м£перы

Важно заметить, что в отношении тока и напряжения термин затухание в том смысле, как он здесь применяется, указывает только на уменьшение амплитуды. Энергия в цепи при этЬм может расходоваться или не расходоваться. Так например, четырехполюсник, изображенный на фиг. 6.17,

имеет разрыв между началом А и концом В. Поэтому при любом Е, значение Еа будет равно нулю; затухание бесконечно и совершенно не зависит от величины сопротивлений или 2, в которых может расходоваться какая угодно мощность.

Кривая, показывающая зависимость затухания от частоты, является основной характеристикой фильтра. Пример такой кривой показан на ф1г 6.18. Соответственно данной кривой амплитуда напряжения на выходе меньше амплитуды на входе при всех co<;o}i, так как затухание положительно. При (о = (Оз затухание равно 3 неп, т. е. амплитуда уменьшается в е раз. При (0 = 0)1 затухание равно нулю. В промежутке между и затухание отрицательно. Это значит, что ампдитуда напряжения на выходе больше, чем на входе. При <о>о)2 затухание вновь становится положительным.

Такая кривая может охарактеризовать четырехполюсник только при определенной нагрузке, к

которой она относится. С изменением нагрузки изменяется и форма кривой Кривая, характеризующая затухание по мощности, имеет, вообще говоря, иную форму, и, как было уже сказано, характеризует четырехполюсник совершенно с другой стороны. Обе кривые совпадут только в том случае, если четырехполюсник со стороны Входа представляется чисто омическим сопротивлением при всех частотах, и если выход также нагружен на чисто омическое сопротивление. Тогда для охарактеризования поведения цепи в зависимости от частоты достаточно одной кривой.

§ 9. Т-образные и П-образные звенья.

Однородный фильтр представляет собой цепочку, составленную из одинаковых звеньев. Каждое звено в свою очередь составляется из последовательных и параллель-

Vzl, Ъ!, %1,

ZJ-rC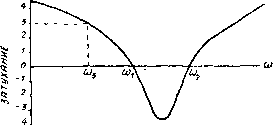

неперы

Фиг. 6.18

ных элементов.

На фиг. 6.19 пока-зана цепочка из Т-образных звеньев. Звено от звена отделено на схеме маленькими кружками.

Элемент j Z называется последовательным о элементом, а элемент Zg - параллельным. Обозначение Zi, а не просто Zi принято для удобства деления всей цепочки на одинаковые элементы. В конструктивном выполнении два рядом стоящие элемента Zj, принад-

Фиг. 6 19.

лежащие на схеме разным звеньям, фактически осуществляются в виде одного элемента Zi.

Звено можйо представить состоящим из двух полузвеньев, как это показа1о, например, на фиг. 6.20, где / и представляют собой полузвенья состоящие из одного последовательного и одного параллельного элеменга.

Зажимы а и & называются Т-образной стороной полузвена, а зажимы с и d - П-образной стороной полузвена.

На фиг. 6.21 показана схема фильтра из П-образных звеньев.

Элемент Zj называется последовательным элементом, а элемент 2Z2 - параллельным. Обозначение 2Z2, а не Z принято по тем же соображениям

I 21,

22, d d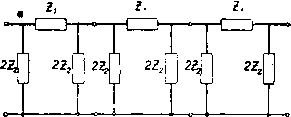

Фиг. 6.20.

Фиг. 6.21.

деления схемы на одинаковые звенья. Конструктивно два параллельных элемента (2Z2) образуют один элемент с сопротивлением Zg.

Комбинация одного параллельного элемента 2Z2 и половины последовательного элемента, т. е. -g-i, называется, как и в предыдущем случае, полузвеном с Т-образными и П-образными сторонами. Таким образом соединением одних и тех же полузвеньев можно получить либо звенья П, либо звенья Т.

§ 10. Исследование фильтров методом четырехполюсника.

В гл. V было показано, что симметрический четырехполюсник, составленный из реактивных элементов, может быть эквивалентно замененлинией единичной длины.

Если Ai, Ag, A3, и А4 представляют собою коэфициенты четырехполюсника (причем Ai = A4), то параметры эквивалентной линии, как было найдено, выразятся Следующим образом.

1) Волновое сопротивление

2) Фазовая постоянная а и постоянная затухания Ь выражаются различно в зависимости от того, лежит ли А в пределах от - 1 до --1 или вне этих пределов. А именно.

При -i<Ai<--l.

а = arc cos (AJ 6 = 0.

В остальных случаях

а = 0 или тс Ь = arc ch (Ai).

Поэтому фильтр, составленный из индуктивных элементов, при нагрузке на сопротивление, равное волновому во всем интервале, где Aj заключено между -1 и --1, пропускает частоты без затухания (6 = 0). Эта область частот называется областью прозрачности фильтра.

в остальной области частот, где ЬфО, существует затухание, обусловленное тем, что отражения внутри звена таковы, что звено не является со стороны входа чисто активным сопротивлением.

Фиг. 6-22.

Рассмотрим в качестве примера цепочку, состоящую из последовательных индуктивных и параллельных емкостных звеньев, схема которой показана на фиг. 6.22.

По табл. V.V четырехполюсников находим

По этому уравнению стрЪим кривую

Ai = F(co).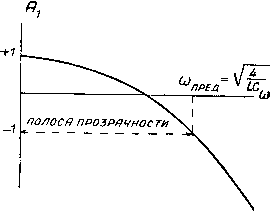

полоса ПРОЗРЙЧНОС ти

(6.10)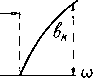

Фиг. 6.23.

Фиг. 6.24.

Эта кривая приведена на фиг. 6.23. Aj лежит в пределах от -1 до4-1 в интервале, в котором частота имеет значение от (о= О до o>npeA = j/

Последняя частота называется предельной частотой. До предельной частоты затухания нет. Далее

Ь = arc ch (Ai).

Зависимость Ь от частоты дана на фиг. 6.24

Если при какой-нибудь частоте о>а b = bk, то это значит, что при этой

частоте амплитуда на выходе меньше амплитуды на входе в е раз. Или, иначе говоря, затухание равно

In - = bk непер.

£>2