Спектр ее выражаете! следующим рядом

\ COS (2u>0 cos (4u>0 cos (6<й<)

2 1 3 3 5 5-7

(0.56)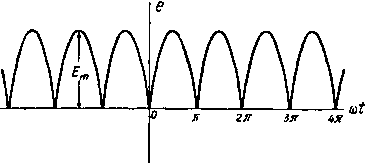

-3Jr -271 -n

Фиг. 0.23.

Спектр ломаной линии, изображенной на фиг. 0.24, выражается рядом 8

Sin {tat) sin (3<o/) , sin (5ш1)

12 32 52

(0.57)

Фиг. 0.24.

Спектр ломаной линии, изображенной на фиг. 0.25, выражается рядом

е==Е

sln( uO , sln(3o)0 , sin(5u)f)

(0.58)

Фиг. О 25.

В трех последних случаях спектр выражается бесконечным рядом, однако, амплитуды вообще быстро убывают с увеличением номера члена, что позволяет ограничиться некоторым конечным числом членов в зависимости от требуемой точности.

Все формулы и графики относятся к периодическим функциям, длящимся от= -сх) до f==--cx). Если данная функция или соответствующая ей

кривая длятся от до /2 то в этом интервале они могут быть также представлены указанными спектрами. Однако теперь эти спектры будут состоять не из синусоид и косинусоид, а из отрезков синусоид и косинусоид умещающихся в интервале от до t.

§ 12. Изображение непериодических явлений при помощи линейчатого спектра.

Цели явление не имеет периодического характера в интервале времени, необходимом для целей данного исследования, то оно не может быть в точности представлено линейчатым спектром. Это ясно из того, что соответствующая ему функция не может быть выражена рядом Фурье.

Однако, как было уже дважды отмечено, наблюдаемое физическое явление не бывает периодичным в строгом смысле этого слова и тем не менее мы можем пользоваться для его изображения пери-одическойфункцией, поскольку оно периодично в течение времени исследования. На этом основании всегда возможно любое и в том числе непериодическое явление представить как периодическое вообразив, что за пределами интервала времени, необходимого для исследования, явление снова повторяется бесчисленное количество раз.

Так например, положим, что кривая фиг. 0.26 соответствует какому нибудь физическому явлению. Допустим, что все интересующие нас последствия от этого явления вполне установились или исчезли по проществии промежутка времени х. (Если кривая фиг. 0.26 изображает эдс в какой-нибудь цепи, то это значит, что ток либо достиг своей стационарной величины и больше не изменяется, либо затух и стал равен нулю).

Тогда ничто не мешает нам допустить, что через промежуток времени Т>х явление снова повторится (фиг. 0.27) и будет повторяться через этот же промежуток времени бесчисленное количество раз. Это дает возможность представить данное явление при помощи линейчатого cneiTpa. Так как промежуток времени Т между воображаемыми повторениями явления не должен быть меньше т, но может быть сколько-угодно больше то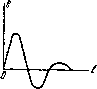

Фиг. О 26.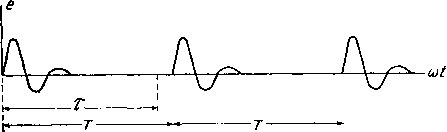

Фиг. 0.27.

очевидно, что можно построить бесчисленное количество различных спектров, выбирая различные интервалы между воображаемыми повторениями явления.

Эти спектры будут соответствовать различным явлениям, но в пределах времени х все эти явления вызовут одинаковые последствия в нашей системе.

Этот способ построения спектра обладает тем недостатком, что он требует предварительного знания минимального промежутка времени, необходимого для того, чтобы в рассматриваемой системе установился режим.

Поэтому им редко пользуются практически. Мы привели его потому, что он может служить мостом для перехода к более сложному представлению о так называемых сплошных спектрах .

§ 13. Понятие о сплошных спектрах.

Положим, что, действуя по способу, изложенному в § 12, мы выбрали промежуток времени Т и представили нашу непериодическую функцию в виде линейчатого спектра, состоящего из бесконечного ряда частот. Часть этого спектра, допустим, изображается графиком фиг. 0.28. По закону образования членов ряда Фурье расстояние между двумя спектральными линиями определится следующим образом. Если Т есть промежуток времени между повторением явления, то этот промежуток времени является вместе с тем основным периодом разложения в ряд Фурье.

Соответствующая ему частота будет

Следующие частоты будут

(О, = 3

. VI т. д.

Теперь с целью уточнить наше разложение увеличим интервал времени между воображаемыми событиями вдвое.

Очевидно прежде всего, что интервал межд соседними частотами уменьшится вдвое, т. е. спектральные линии станут чаще. Во-вторых, амплитуда каждой составляющей ча-

лмплитуды при sm (или cosj ня учйстке спекгря ПРИ периоде Рйзломения J

Фиг. 0.28.

рмппитуаы ПРИ sin (или cos) нй у чистке спвктрй ПРИ пеРиопе Рйзложения

Фиг. 0.29.

стоты уменьшится, так как энергия, приходившаяся раньше на какую-нибудь группу из п линий, распределится теперь между числом линий, равным 2п, в том же интервале частот.

Участок спектра, соответствующий фиг. 0.28, примет теперь вид фиг. 0.29.

Если снова и снова удваивать интервал времени между воображаемыми повторениями явления, то спектр будет все более и более точно выражать явления. Спектральные линии будут все более и более тесно сближаться. Амплитуда их будет стремиться к нулю по Mej)e того, как интервал Т будет стремиться к бесконечности.

Если бы оставить масштаб чертежа неизменным, то уменьшение амплитуд приведет в конце концов к тому, что их нельзя уже будет графически изобразить на чертеже. Чтобы обойти это затруднение, можно при каждом удвоении промежутка времени изменять вертикальный масштаб чертежа также вдвое, достигая этим примерного сохранения высоты вертикальных линий. По мере того, как промежуток времени Т будет стремиться к бесконечности, масштаб будет также стремиться к бесконечности, т. е. конечными отрезками будут изображаться бесконечно малые величины.

Нам нет надобности при этом вычерчивать все отдельные вертикальные палочки, да это вскоре станет и невозможным, так как все они сольются. Достаточно начертить только огибающую, проходящую по их вершинам.

При бесконечном увеличении промежутка времени Т эта огибающая стремится к определенному предельному положению. Она может быть вычислена аналитически посредством так называемого двойного интеграла Фурье, если вид функции, выражающей явление, задан.