приравняв значение каждого коэфициента А, стоящее во второй колонне таблицы, соответствующему значению того же А, стоящему в третьей колонне, получим четыре уравнения.

Решив эти уравнения относительно Z, з, з, получим

a + ft + c ~2,-rZ,H-Z,

(5.56)

где Za,6,c==

a, b, с

Ур-ния (5.56) дают возможность найти те сопротивления Z, з, з, из которых надо составить Т-образную схему, эквивалентную П-образной с задан-

ными значениями Za, c==v-

a,b,c

Решив те же ур-ния относительно Уд,&, с, найдем

У2У3

Ус =

УхУг

{5.57}

Ух+Уг + П

где У1, з,з = -7-.

1* 2* 3

Ур-ния (5.57) позволяют найти проводимости, которые надо включить по П-образной схеме для того, чтобы эквивалентно заменить Т-образную схему.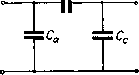

Фиг. 5.21.

В частности, например, Т-образный четырехполюсник, составленный из. конденсаторов Cj, С3, С3 (фиг. 5.21) эквивалентно заменяется П-образным четырехполюсником с емкостями Са, Сь, Сг, если

С2С,

Сг. =

С,Сз

-c. + c-f Сз Для обратной замены должно быть

(5.58)

с,с, + с,с-\-с,с,

Ьз---

(5.59)

Для того чтобы написать те же формулы для четырехполюсников, составленных из самоиндукций, надо замекить букву С буквой L, индексы а, b VI с индексами 1, 2, 3, и обратно - индексы 1, 2, 3 - индексами а, Ь, с.

В рассмотренном примере, когда четырехполюсник составлен только из однородных индуктивных элементов (L или С), частота не входит в написанные уравнения. Поэтому эквивалентность Т- и П-образной схемы не зависит от частоты.

Такой же результат получится и в том случае, если четырехполюсник состоит только из омических сопротивлений.

Если же в схему входят хотя бы два разнородных элемента, т. е. С и L или L и R или С и /?, в ур-ниях (5.56) или (5.57), служащих для вычисления эквивалентных элементов Z, Z, Zg или Vi, У, Уз, появится множитель частоты.

Разумеется, в этом случае одна схема будет эквивалентна другой только пр1 той частоте, для которой сделано вычисление по ур-ниям (5.56) или (5.57).

§ 12. Эквивалентная замена однородной линии четырехполюсником с сосредоточенными постоянными и обратная замена.

В гл. II § 17 были выведены следующие уравнения для однородной двухпроводной линии:

Ех == Ео ch (/ах + рх) + р/о sh (/хх + рх)

Sh (/аХ 4- рх) -[- /о ch (/ах -\- fx)

(5.60)

Фиг . 5.22.

Эти уравнения дают возможность определить значения тока и напряжения 1хИ Еху входных зажимов (фиг. 5.22), если известны ток и напряжение /о и у выходных зажимов линии. Напомним, что в этих уравнениях

и называется фазовым коэфициентом

и называется километрическим коэфициентом затухания.

R предйтавляет собой последовательное сопротивление, а g-утечку (проводимость), равномерно распределенные вдоль линии, но рассчитанные на 1 км длины линии,

и называется волновым сопротивлением линии. Наконец, сумма (/a-f p) = Y

называется постоянной распространения линии.

Заменим в ур-нии (5.60) индексы хиОна 1 и 2 с тем, чтобы придать этому уравнению ту форму, которой мы пользовались для четырехполюсника, и положцм X, т. е. длину линии, равной единице.

Получим

/1 = 2

shCT)

+ /2 [ch(T)]

(5.61)

Ур-ние (5.61) показывает, что если .линию единичной длины рассматривать как четырехполюсник, то параметрами последнего будут величины, стоящие в прямых скобках, т. е.

Ai = A4 = ch(r) \

Аз = / sh(T) A3=]/i;sh(T)

(5.62)

причем т = (/ + Р)-

Поэтому каждая данная линия может быть эквивалентно заменена четырехполюсником с сосредоточенными постоянными, если параметры последнего соответствуют ур-нию (5.62).

Можно поступить и обратно и заменить симметричный четырехполюсник эквивалентной двухпроводной линией единичной длины.

Такая замена оказывается очень плодотворной в теории фильтров. Тогда взамен параметров А четырехполюсник может быть охарактеризован параметрами, аналогичными по формальному смыслу параметрам а, р, и

Эти параметры мы, однако, для отличия обозначим другими буквами, как это показано в следующей табл. V. VII.

Таблица V.VII