при заданной частоте Ai, Ag, A3 и А4 являются величинами постоянными, а вообще являются некоторыми функциями частоты.

В простейших случаях не представляет труда определить параметры четырехполюсника, исходя из закона Кирхгофа. Для более сложных случаев применяются особые приемы, которые будут указаны ниже.

Так например, пусть требуется сделать такое вычисление для четырехполюсника, схема которого показана на

фиг, 5.7. Положим сначала, что энергия передается слева направо. На основании закона Кирхгофа пишем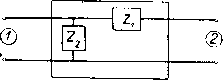

Фиг. 5.7.

/1 = /2 + /з

(5.4)

Решая эти уравнения относительно /j и Е, получаем

/1 = 2 + /2 2

(5.5)

Из сопоставления написанных уравнений с ур-нием (5.3) очевидно, что

Ai = l+f A2 = Zi

A.,= i-

(5.6)

Если поменять ролью зажимы данного четырехполюсника, т. е. рассмотреть случай, кбгда энергия передается справа налево, тем же путем найдем

Ai=l

A2 = Zi

A3 - у

(5.7)

Сравнение ур-ний (5.6) и (5.7) показывает, что коэфициенты Аа и A3 остались без изменения, а коэфициенты Ai и А4 поменялись местами.

Это правило остается действительным для рассматриваемых четырехполюсников также и при любой другой схеме.

§ 4. Зависимость между коэфициентами четырехполюсника.

Положим, что на входе четырехполюсника приложено сначала некоторое напряжение Е с частотой coi, а затем другое напряжение с ча-

стотой о>2. Пусть соответствующие токи будут /j и I. Так как частоты o)i и о>2 различны, то вообще

eJx -ЕхКфО. (5.8)

Аналогично можно написать и для напряжения и тока на выходе

1 \

Если Е имеет частоту o>j, а Eg частоту Шд, то

еХ - Ё21\Ф0. (5.9)

Всегда, однако, можно подобрать значения Е и Ег такими, чтобы

Е, -V/i-44 + 4>2 = 0. (5.10)

Исключим теперь из ур-ния (5.10) Ej, /j, Ei и Д, подставив их значения из основного уравнения четырехполюсника, т. е.

Ej = AjEg -j- Ag/g

a также

E/ = AiE2 + A

= АзЁ2 + аЛ.

Получим после приведения подобных членов следующее выражение

(А1А4 - А2А3 - 1) (Eg/g - Е/з) = 0. (Ъ. 11)

Так как множитель, заключенный во вторые скобки, вообще не равен нулю, то множитель, заключенный в первые скобки, всегда должен быть* равен нулю. Следовательно,

AiA4-AA=l- (5.12)

Это замечательное соотношение показывает, что для определения пассивного линейного четырехполюсника вообще достаточно трех параметров, так как четвертый может быть определен из ур-ния (5.12).

§ 5. Симметричные и несимметричные четырехполюсники.

Если даны уравнения четырехполюсника в обычной форме

EiAiEa + A/; /1 = А3Е2 -j- А4/2

(5.13)

легко написать уравнения для определения Е и 1. Решив ур-ние (5.13) относительно Ео и 1 и приняв во внимание, что

AiA4-A2A3=l, (5.14)

получим

E2 = A4Ei-f-A2/i

(5.15)

4 = A3Ei-f-Ai/i

ур-ние (5.15) показывает, что по сравнению с ур-нием (5.13) коэфициенты Aj и А4 поменялись местами, а коэфициенты Аз и A3 остались без изменения.

С этим правилом мы уже встретились в § 4 на частном примере. Таким образом в общем случае переход энергии слева направо (фиг, 5.8) (когда зажимы 7 являются входными зажимами) отличается от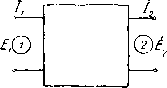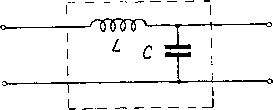

Фиг. 5.8.

Фиг. 5-9.

перехода энергии справо налево (когда зажимы 2 являются входными зажимами).

Такой четырехполюсник называется несимметричным. Примером несимметричного четырехполюсника является схема фиг. 5.9. Два несимметричных четырехполюсника, включенные навстречу друг другу, образуют симметричный четырехполюсник.

На фиг. 5.10 показан симметричный четырехполюсник, образованный из несимметричных, типа фиг. 5,9,

В симметричном четырехполюснике передача энергии слева направо происходит так же, как и справа налево. Поэтому ур-ния (5.13) и (5,15)

L L

(рпвноу

Фиг, 5,10.

должны дать тождественные результаты. Для этого Ai должно быть равно А4.

Поэтому взаимная связь между коэфициентами, выражаемая ур-нием (5.14), напишется теперь так

Ai2-A2A3 = 1, (5.16)

так как

Ai = А4.

§ 6. Определение параметров симметричного четырехполюсника посредством измерения.

Назовем входным сопротивлением четырехполюсника отношение

A = z

Так же выходным сопротивлением назовем отношение

4?-= 2,.