Каждой периодической функций соответствует свой единственный график и каждому графику - своя единственная периодическая функция.

Всякое изменение вида функции тотчас же отразится на изменении ее спектра, и наоборот.

Поэтому, какие бы сложные превращения форм эдс и тока ни производились в радиотехнических цепях, все они в конечном итоге могут быть сведены к тем либо другим видоизменениям (или, как говорят, трансформациям ) спектров.

Поэтому спектр является весьма важной характеристикой физических величин, изменяющихся во времени. Как мы увидим далее, очень часто истинный вид функции может и не представлять для нас интереса, и все необходимые выводы можно сделать исключительно на основании характера спектра.

Представление 6 периодической функции необходимо уточнить так же, как было раньше уточнено представление о синусоидальной функции. Если, функция периодична в математическом смысле слова, то она продолжается от t = - oo до t = -{-oo, т. е. всегда.

В действительности мы не мужем наблюдать физических явлений, соответствующих этому усювию.

Физическое явление может иметь периодический характер только в течение некоторого времени. Следовательно, на опыте мы имеем дело с явлениями периодическими в пределах некоторого интервала времени.

Однако, если этот интервал длится более того времени, в течение которого производится или мыслится исследование, то для этого исследования совершенно безразлично, повторяется ли данное явление периодически до бесконечности или кончается вслед за тем, как закончено наше исследование. Это дает нам право представлять явление посредством периодической функции. Спектр этой периодической функции мы в праве представлять в указанной выше форме, т. е. в виде суммы подлинных синусоид и косинусоид, длящихся от ti=~ оо ло t = -{-oo.

Рассмотренный здесь вид спектра носит название линейчатого спектра .

Линейчатый спектр, следовательно, применим только для случаев, когда физическое явление может быть описано периодической функцией. Способы спектрального представления явлений в других случаях укажем ниже, а пока рассмотрим несколько примеров линейчатых спектров.

§11. Примеры линейчатых спектров.

а) Спектр кривой, образованной суммой двух косинусоид равной амплитуды и фазы, но различной частоты (< , и щ), может быть изображен уравнением

е = Ет [cos (a)iO -f cos ((OjjO] (0.49)

или, наконец, символическим уравнением

Е Ет (e-i-f е- 0- (0-50)

Последнее уравнение особенно удобно использовать, чтобы проанализировать получающуюся кривую с точки зрения ее формы. Положив

а>2 = О) - Д,

перепишем это уравнение так

Е = Ет[е +) + е Ч -)] = Ят (е + е-0 е =

= [ЕтС08(Ще*. (0.51)

Выражение, стоящее в прямых скобках, можно рассматривать как амплитуду, которая во времени изменяетсяинусоидально с частотой Л.

Когда cos (Д/) == 1, амплитуда достигает значения 2Ет Когда cos (Af) =s О - амплитуда равна нулю. Так как в этот момент косинус меняет знак, то, следовательно, фаза колебания поворачивается на 180°.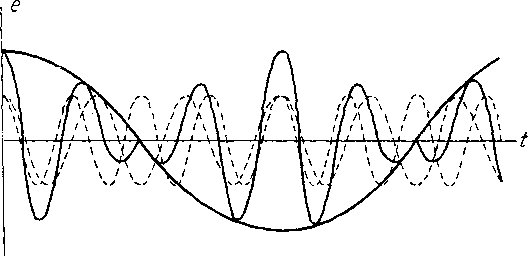

Фиг. 0.17.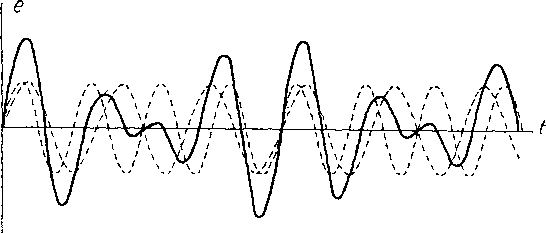

Фиг. 0.18.

Частота колебания определяется величиной

0>

(0.52)

Такая кривая изображена на фиг. 0.17. Жирная огибающая линия является косинусоидой. Нд фиг. 0.18 показано сложение двух синусоид. вмплитуды ПРИ косинусй?- б) Спектр кривой, образованной тремя косину-

соидами,

еЕт cos (ш/) 4- cos (со 4- А) / cos (со - Д) f, (0.53)

графически изобразится фиг. 0.19. В символической форме получим

(d-l) и (и+й) Фиг. 0.19.

ЕЕе -{--~[eJ (-+) + е ]. (0.54)

Это можно преобразовать так

Е=={Ет [1+С08(Д/)]}еЧ

(0.55)

Рассматриваем выражение, стоящее в прямых скобках, как амплитуду, изменяющуюся- во времени уже не по закону cos (Л/), а по закону [1 -\- cos (Af)]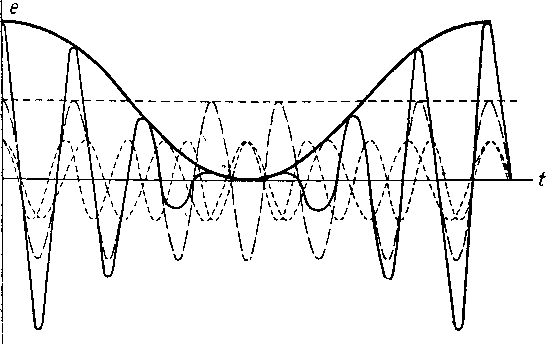

Фиг. 0.20.

Следовательно, амплитуда изменяется от нуля до двойной величины по сравнению с Ет, но не меняет знака. Кривая имеет вид, показанный сплошной линией на фиг. 0.20. Жирная огибающая кри- вая является косинусоидой. Кривая, соответствующая спектру фиг.0.21, в которой амплитуды, соответствующие часто-

амплитудьг при косинусях

Фиг.ГО.21.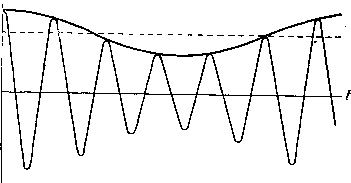

Фиг. 0.22.

там ((o-f-A) и (о) -Д), меньше половины амплитуды при частоте ш, показана на фиг. 0.22. Огибающая ее также косинусоида, но амплитуда этой косинусоиды меньше Ет-

в) На фиг. 0.23 показана кривая, состоящая из периодически повторяющихся отрезков синусоиды в интервале от О до тс.